【题目】如图,图中二次函数解析式为y=ax2+bx+c(a≠0)则下列命题中正确的有(填序号).①abc>0;②b2<4ac;③4a﹣2b+c>0;④2a+b>c.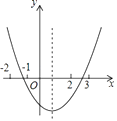
参考答案:
【答案】①③④
【解析】①∵抛物线开口向上,抛物线的对称轴在y轴右侧,抛物线与y轴交于负半轴,
∴a>0,![]() >0,c<0,
>0,c<0,
∴b<0,abc>0,①正确;
②∵抛物线与x轴有两个不同交点,
∴![]() =b2-4ac>0,b2>4ac,②正确;
=b2-4ac>0,b2>4ac,②正确;
③当x=-2时,y=4a-2b+c>0,③正确;
④∵0<![]() <1,
<1,
∴-2a<b<0,
∴2a+b>0>c,④正确.
所以答案是:①③④.
【考点精析】解答此题的关键在于理解二次函数图象以及系数a、b、c的关系的相关知识,掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,∠COD=90°,直线AB与OC交于点B,与OD交于点A,射线OE与射线AF交于点G.若OE将∠BOA分成1︰2两部分,AF平分∠BAD,∠ABO=
 (30°<
(30°<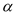 <90°) ,则∠OGA的度数为(用含
<90°) ,则∠OGA的度数为(用含 的代数式表示)____________________.
的代数式表示)____________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知抛物线与直线的图象如图所示,当y1≠y2时,取y1 , y2中的较大值记为N;当y1=y2时,N=y1=y2 . 则下列说法:
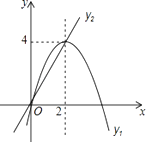
①当0<x<2时,N=y1;
②N随x的增大而增大的取值范围是x<0;
③取y1 , y2中的较小值记为M,则使得M大于4的x值不存在;
④若N=2,则x=2﹣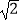 或x=1.
或x=1.
其中正确的有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】某手机店销售
 部
部 型和
型和 部
部 型手机的利润为
型手机的利润为 元,销售
元,销售 部
部 型和
型和 部
部 型手机的利润为
型手机的利润为 元.
元.(1)求每部
 型手机和
型手机和 型手机的销售利润;
型手机的销售利润;(2)该手机店计划一次购进
 ,
, 两种型号的手机共
两种型号的手机共 部,其中
部,其中 型手机的进货量不超过
型手机的进货量不超过 型手机的
型手机的 倍,设购进
倍,设购进 型手机
型手机 部,这
部,这 部手机的销售总利润为
部手机的销售总利润为 元.
元.①求
 关于
关于 的函数关系式;
的函数关系式;②该手机店购进
 型、
型、 型手机各多少部,才能使销售总利润最大?
型手机各多少部,才能使销售总利润最大?(3)在(2)的条件下,该手机店实际进货时,厂家对
 型手机出厂价下调
型手机出厂价下调 元,且限定手机店最多购进
元,且限定手机店最多购进 型手机
型手机 部,若手机店保持同种手机的售价不变,设计出使这
部,若手机店保持同种手机的售价不变,设计出使这 部手机销售总利润最大的进货方案.
部手机销售总利润最大的进货方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABD和∠BDC的平分线相交于点E,BE交CD于点F,∠1+∠2=90°.试说明:(1)直线AB//CD.(2) 如果∠1=55°,求∠3的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在8×8的正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的顶点都在正方形网格的格点上.
(1)将△ABC经平移后得到△A′B′C′,点A的对应点是点A′.画出平移后所得的△A′B′C′;
(2)连接AA′、CC′,则四边形AA′C′C的面积为 ________.
(3)若连接AA′,BB′,则这两条线段之间的关系是 ;
(4)△ABC的高CD所在直线必经过图中的一个格点点P,在图中标出点P.

-
科目: 来源: 题型:
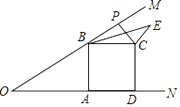
查看答案和解析>>【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为 .
相关试题

