【题目】如图,在8×8的正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的顶点都在正方形网格的格点上.
(1)将△ABC经平移后得到△A′B′C′,点A的对应点是点A′.画出平移后所得的△A′B′C′;
(2)连接AA′、CC′,则四边形AA′C′C的面积为 ________.
(3)若连接AA′,BB′,则这两条线段之间的关系是 ;
(4)△ABC的高CD所在直线必经过图中的一个格点点P,在图中标出点P.

参考答案:
【答案】(1)见解析;(2)6;(3)平行且相等;(4)见解析
【解析】
(1)直接利用平移的性质得出对应点位置进而得出答案;
(2)AA′平行且等于CC′,AA′C′C是平行四边形,直接利用割补法求面积即可.
(3)由平移的性质可得AA′与BB′平行且相等;
(4)过C作AB的垂线即可;
(1)如图所示:

(2)由平移的性质可得:AA′平行且等于CC′,AA′C′C是平行四边形,
利用割补求得![]()
故答案是:6;
(3)由平移的性质可得:AA′与BB′平行且相等,
故答案是:平行且相等;
(4)过C作AB的垂线,P点位置如图;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某手机店销售
 部
部 型和
型和 部
部 型手机的利润为
型手机的利润为 元,销售
元,销售 部
部 型和
型和 部
部 型手机的利润为
型手机的利润为 元.
元.(1)求每部
 型手机和
型手机和 型手机的销售利润;
型手机的销售利润;(2)该手机店计划一次购进
 ,
, 两种型号的手机共
两种型号的手机共 部,其中
部,其中 型手机的进货量不超过
型手机的进货量不超过 型手机的
型手机的 倍,设购进
倍,设购进 型手机
型手机 部,这
部,这 部手机的销售总利润为
部手机的销售总利润为 元.
元.①求
 关于
关于 的函数关系式;
的函数关系式;②该手机店购进
 型、
型、 型手机各多少部,才能使销售总利润最大?
型手机各多少部,才能使销售总利润最大?(3)在(2)的条件下,该手机店实际进货时,厂家对
 型手机出厂价下调
型手机出厂价下调 元,且限定手机店最多购进
元,且限定手机店最多购进 型手机
型手机 部,若手机店保持同种手机的售价不变,设计出使这
部,若手机店保持同种手机的售价不变,设计出使这 部手机销售总利润最大的进货方案.
部手机销售总利润最大的进货方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图中二次函数解析式为y=ax2+bx+c(a≠0)则下列命题中正确的有(填序号).①abc>0;②b2<4ac;③4a﹣2b+c>0;④2a+b>c.
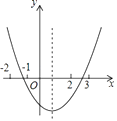
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABD和∠BDC的平分线相交于点E,BE交CD于点F,∠1+∠2=90°.试说明:(1)直线AB//CD.(2) 如果∠1=55°,求∠3的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为 .
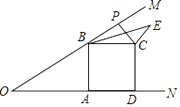
-
科目: 来源: 题型:
查看答案和解析>>【题目】有足够多的长方形和正方形卡片,如下图:

(1)如果选取1号、2号、3号卡片分别为l张、1张、2张,可拼成一个长方形(不重叠无缝隙),请画出这个长方形(所画图形大小和原图保持一致),并用等式表示拼图前后面积之间的关系:
(2)小明用类似方法解释分解因式a2+5ab+4b2,请画图说明小明的方法(所画图形大小和原图保持一致),并写出分解因式的结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元。
(1)求购买一个足球、一个篮球各需多少元?
(2)根据学校实际情况,需从体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?
相关试题

