【题目】如图,AC平分∠DAB,CE⊥AB于E,AB=AD+2BE,下列结论正确的有( )个
①AE= ![]() (AB+AD); ②∠DAB+∠DCB=180°; ③CD=CB;④S△ACE﹣S△BCE=S△ADC;⑤AD=AE.
(AB+AD); ②∠DAB+∠DCB=180°; ③CD=CB;④S△ACE﹣S△BCE=S△ADC;⑤AD=AE.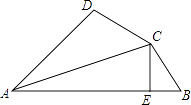
A.2个
B.3个
C.4个
D.5个
参考答案:
【答案】D
【解析】解:①在AE取点F,使EF=BE,
∵AB=AD+2BE=AF+EF+BE,EF=BE,
∴AB=AD+2BE=AF+2BE,
∴AD=AF,
∴AB+AD=AF+EF+BE+AD=2AF+2EF=2(AF+EF)=2AE,
∴AE= ![]() (AB+AD),故①正确;
(AB+AD),故①正确;
②在AB上取点F,使BE=EF,连接CF.
在△ACD与△ACF中,∵AD=AF,∠DAC=∠FAC,AC=AC,
∴△ACD≌△ACF,
∴∠ADC=∠AFC.
∵CE垂直平分BF,
∴CF=CB,
∴∠CFB=∠B.
又∵∠AFC+∠CFB=180°,
∴∠ADC+∠B=180°,
∴∠DAB+∠DCB=360﹣(∠ADC+∠B)=180°,故②正确;
③由②知,△ACD≌△ACF,∴CD=CF,
又∵CF=CB,
∴CD=CB,故③正确;
④易证△CEF≌△CEB,
∴S△ACE﹣S△BCE=S△ACE﹣S△FCE=S△ACF ,
又∵△ACD≌△ACF,
∴S△ACF=S△ADC ,
∴S△ACE﹣2S△BCE=S△ADC , 故④正确.
⑤由①知,AD=AF,且AF<AE,所以AD<AE,故⑤错误.
故选D.
【考点精析】认真审题,首先需要了解角的平分线(从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线),还要掌握线段垂直平分线的性质(垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等)的相关知识才是答题的关键.
-
科目: 来源: 题型:
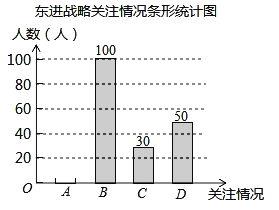
查看答案和解析>>【题目】深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图表的一部分如下:

(1)根据上述统计图可得此次采访的人数为 人,m= ,n= ;
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,请估计在15000名深圳市民中,高度关注东进战略的深圳市民约有 人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据等式的性质,下列各式的变形中,一定正确的是( )
A. 若a=b,则a+c=b-c B. 若a=b+2,则3a=3b+6
C. 若6a=2b,则a=3b D. 若ac=bc,则a=b
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果方程x2+px+q=0的两个根是x1 , x2 , 那么x1+x2=﹣p,x1x2=q,请根据以上结论,解决下列问题:
(1)若p=﹣4,q=3,求方程x2+px+q=0的两根.
(2)已知实数a、b满足a2﹣15a﹣5=0,b2﹣15b﹣5=0,求 +
+ 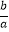 的值;
的值;
(3)已知关于x的方程x2+mx+n=0,(n≠0),求出一个一元二次方程,使它的两个根分别是已知方程两根的倒数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=(x+1)2+1,当x<_____时,y随x的增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列不等式(组),并把解集在数轴上表示出来.
(1)2x﹣1>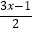
(2)
. -
科目: 来源: 题型:
查看答案和解析>>【题目】每年5月的第二周为“职业教育活动周”,今年我省开展了以“弘扬工匠精神,打造技能强国”为主题的系列活动.活动期间某职业中学组织全校师生并邀请学生家长和社区居民参加“职教体验观摩”活动,相关职业技术人员进行了现场演示,活动后该校教务处随机抽取了部分学生进行调查:“你最感兴趣的一种职业技能是什么?”并对此进行了统计,绘制了统计图(均不完整).请解答以下问题:
(1)补全条形统计图和扇形统计图;
(2)若该校共有1800名学生,请估计该校对“工业设计”最感兴趣的学生有多少人?
(3)要从这些被调查的学生中,随机抽取一人进行访谈,那么正好抽到对“机电维修”最感兴趣的学生的概率是 .

相关试题

