【题目】已知直线BC//ED.
(1)如图1,若点A在直线DE上,且∠B=44°,∠EAC=57°,求∠BAC的度数;
(2)如图2,若点A是直线DE的上方一点,点G在BC的延长线上求证:∠ACG=∠BAC+∠ABC;
(3)如图3,FH平分∠AFE,CH平分∠ACG,且∠FHC比∠A的2倍少60°,直接写出∠A的度数.



参考答案:
【答案】(1)79°;(2)见解析;(3)40°
【解析】分析:(1)由平行线的性质得到∠BAE+∠B=180°,∠EAC=∠C,再由平角的定义即可得到结论;
(2)作AF//BC,得到AF//ED//BC,再由平行线的性质得到∠FAC =∠ACG ,∠ABC=∠FAB,即可得到结论;
(3)作AM//BC,HN//BC, 得到AM//BC//ED,HN//BC//ED,
又设∠ACH=∠GCH=x, ∠AFH=∠EFH =y,则有∠A=2x-2y, ∠FHC=x-y,得到∠A=2∠FHC,又已知∠FHC=2∠A-60°,即可得到结论.
详解:(1)∵BC//ED,∴∠BAE+∠B=180°,∠EAC=∠C,∴∠BAC=180°-∠B-∠EAC=79°;
(2)如图,作AF//BC.又∵BC//ED,∴AF//ED//BC,
∴∠FAC =∠ACG ,且∠ABC=∠FAB,∴∠ACG=∠FAC=∠BAC+∠FAB=∠BAC+∠ABC.

(3)作AM//BC,HN//BC, ∴可证AM//BC//ED,HN//BC//ED,
又设∠ACH=∠GCH=x, ∠AFH=∠EFH =y,
∴∠A=2x-2y, ∠FHC=x-y,
∴∠A=2∠FHC,
又∵∠FHC=2∠A-60°,
∴∠A=40°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c的图象如图所示,则下列四个结论:①a+b+c<0;②a+c=b;③b=﹣2a;④4ac﹣b2<0,其中正确的结论有( )
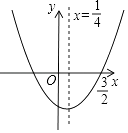
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系中,
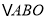 的面积为8,
的面积为8,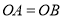 ,
,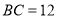 ,点
,点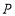 的坐标是
的坐标是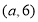 .
.(1)求
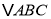 三个顶点
三个顶点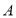 、
、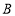 、
、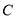 的坐标;
的坐标;(2)若点
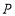 坐标为
坐标为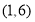 ,连接
,连接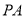 ,
,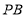 ,求
,求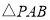 的面积;
的面积;(3)是否存在点
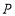 ,使
,使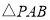 的面积等于
的面积等于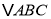 的面积?如果存在,请求出点
的面积?如果存在,请求出点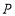 的坐标.
的坐标.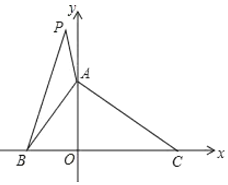
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣14+(2016﹣π)0﹣(﹣
 )﹣1+|1﹣
)﹣1+|1﹣ 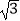 |﹣2sin60°.
|﹣2sin60°. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,四边形OABC为矩形,点A的坐标为(4,0),点B的坐标为(4,3),动点M,N分别从O、B同时出发,以每秒1个单位长度的速度运动,其中,点M沿OA向终点A运动,点N沿BC向终点C运动,过点M作MP⊥OA,交AC于P,连接NP.下列说法①当点M运动了2秒时,点P的坐标为(2,
 );②当点M运动
);②当点M运动  秒时,△NPC是等腰三角形;③当点N运动了2秒时,△NPC的面积将达到最大值.其中正确的有 .
秒时,△NPC是等腰三角形;③当点N运动了2秒时,△NPC的面积将达到最大值.其中正确的有 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市投入31500元购进A、B两种饮料共800箱,饮料的成本与销售价如下表:(单位:元/箱)
类别
成本价
销售价
A
42
64
B
36
52
(1)该超市购进A、B两种饮料各多少箱?
(2)全部售完800箱饮料共盈利多少元?
相关试题

