【题目】二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为 . 
参考答案:
【答案】3
【解析】方法一解:∵抛物线的开口向上,顶点纵坐标为﹣3,
∴a>0.
﹣ ![]() =﹣3,即b2=12a,
=﹣3,即b2=12a,
∵一元二次方程ax2+bx+m=0有实数根,
∴△=b2﹣4am≥0,即12a﹣4am≥0,即12﹣4m≥0,解得m≤3,
∴m的最大值为3,
方法二:解:一元二次方程ax2+bx+m=0有实数根,则二次函数y=ax2+bx的图象与直线y=﹣m有交点,
由图象得,﹣m≥﹣3,解得m≤3,
∴m的最大值为3,
故答案为3.
方法一、由抛物线的开口向上,顶点纵坐标为﹣3得出b2=12a,利用根的判别式,即可求得m的取值范围;方法二、一元二次方程ax2+bx+m=0有实数根,则二次函数y=ax2+bx的图象与直线y=﹣m有交点,根据图像易求出m的取值范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地新建的一个企业,每月将生产1960吨污水,为保护环境,该企业计划购置污水处理器,并在如下两个型号种选择:
污水处理器型号
A型
B型
处理污水能力(吨/月)
240
180
已知商家售出的2台A型、3台B型污水处理器的总价为44万元,售出的1台A型、4台B型污水处理器的总价为42万元.
(1)求每台A型、B型污水处理器的价格;
(2)为确保将每月产生的污水全部处理完,该企业决定购买上述的污水处理器,那么他们至少要支付多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是交警在一个路口统计的某个时段来往车辆的车速(单位:千米/时)情况.

(1)这些车的平均速度为__________千米/时;
(2)车速的众数是__________;
(3)车速的中位数是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的直径为10cm,则圆柱上M,N两点间的距离是cm.
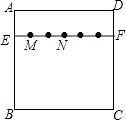
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c的图象如图所示,则下列四个结论:①a+b+c<0;②a+c=b;③b=﹣2a;④4ac﹣b2<0,其中正确的结论有( )
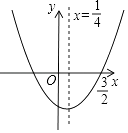
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系中,
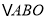 的面积为8,
的面积为8,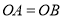 ,
,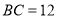 ,点
,点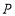 的坐标是
的坐标是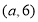 .
.(1)求
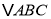 三个顶点
三个顶点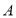 、
、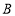 、
、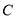 的坐标;
的坐标;(2)若点
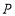 坐标为
坐标为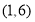 ,连接
,连接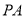 ,
,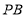 ,求
,求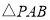 的面积;
的面积;(3)是否存在点
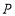 ,使
,使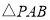 的面积等于
的面积等于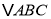 的面积?如果存在,请求出点
的面积?如果存在,请求出点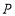 的坐标.
的坐标.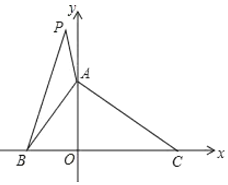
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线BC//ED.
(1)如图1,若点A在直线DE上,且∠B=44°,∠EAC=57°,求∠BAC的度数;
(2)如图2,若点A是直线DE的上方一点,点G在BC的延长线上求证:∠ACG=∠BAC+∠ABC;
(3)如图3,FH平分∠AFE,CH平分∠ACG,且∠FHC比∠A的2倍少60°,直接写出∠A的度数.



相关试题

