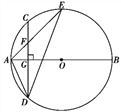
【题目】如图,AB是☉O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]() =
=![]() ,连接AF并延长交☉O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=3;③tan∠E=
,连接AF并延长交☉O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=3;③tan∠E=![]() ;④S△ADF=6
;④S△ADF=6![]() .
.
其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】A
【解析】分析:①利用垂径定理可知![]() ,可知∠ADF=∠AED,结合公共角可证明△ADF∽△AED;②结合CF=2,且
,可知∠ADF=∠AED,结合公共角可证明△ADF∽△AED;②结合CF=2,且![]() ,可求得DF=6,且CG=DG,可求得FG=2;③在Rt△AGF中可求得AG,在Rt△AGD中可求得tanADG=
,可求得DF=6,且CG=DG,可求得FG=2;③在Rt△AGF中可求得AG,在Rt△AGD中可求得tanADG=![]() ,且∠E=∠ADG,可判断出③;④可先求得S△ADF,再求得△ADF∽△AED的相似比,可求出S△ADE=7
,且∠E=∠ADG,可判断出③;④可先求得S△ADF,再求得△ADF∽△AED的相似比,可求出S△ADE=7![]() .
.
详解:①∵AB为直径,AB⊥CD,
∴![]() ,
,
∴∠ADF=∠AED,且∠FAD=∠DAE,
∴△ADF∽△AED,
∴①正确;
②∵AB为直径,AB⊥CD,
∴CG=DG,
∵![]() ,且CF=2,
,且CF=2,
∴FD=6,
∴CD=8,
∴CG=4,
∴FG=CG-CF=4-2=2,
∴②错误;
③在Rt△AGF中,AF=3,FG=2,
∴AG=![]() ,且DG=4,
,且DG=4,
∴tan∠ADG=![]() ,
,
∵∠E=∠ADG,
∴tan∠E=![]() ,
,
∴③错误;
④在Rt△ADG中,AG=![]() ,DG=4,
,DG=4,
∴AD=![]() ,
,
∴![]() ,
,
∴△ADF∽△AED中的相似比为![]() ,
,
∴![]() ,
,
在△ADF中,DF=6,AG=![]() ,
,
∴S△ADF=![]() DFAG=
DFAG=![]() ×6×
×6×![]() =3
=3![]() ,
,
∴![]() ,
,
∴S△ADE=7![]() ,
,
∴④错误;
∴正确的有①一个.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=﹣x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,OB=OC=3,直线l是抛物线的对称轴,E是抛物线的顶点.
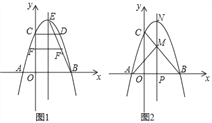
(I)求b,c的值;
(Ⅱ)如图1,连BE,线段OC上的点F关于直线l的对称点F′恰好在线段BE上,求点F的坐标;
(Ⅲ)如图2,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M、与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?若存在,求出点Q的坐标;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学中,运用整体思想方法在求代数式的值中非常重要.
例如:已知:a2+2a=1,则代数式2a2+4a+4=2( a2+2a) +4=2×1+4=6.
请你根据以上材料解答以下问题:
(1)若
 ,求
,求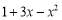 的值;
的值;(2)当
 时,代数式
时,代数式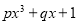 的值是5,求当
的值是5,求当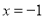 时,代数式px3+qx+1的值;
时,代数式px3+qx+1的值;(3)当
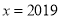 时,代数式
时,代数式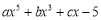 的值为m,求当
的值为m,求当 时,求代数式
时,求代数式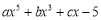 的值是多少?
的值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数
碟子的高度(单位:cm)
1
2
2
2+1.5
3
2+3
4
2+4.5
…
…

(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
 与一次函数y=k2x-k2+2在同一直角坐标系中的图象相交于A,B两点,其中A(-1,3),直线y=k2x-k2+2与坐标轴分别交于C,D两点,下列说法:①k1,k2<0;②点B的坐标为(3,-1);③当x<-1时,
与一次函数y=k2x-k2+2在同一直角坐标系中的图象相交于A,B两点,其中A(-1,3),直线y=k2x-k2+2与坐标轴分别交于C,D两点,下列说法:①k1,k2<0;②点B的坐标为(3,-1);③当x<-1时, <k2x-k2+2;④tan∠OCD=-
<k2x-k2+2;④tan∠OCD=-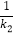 ,其中正确的是( )
,其中正确的是( )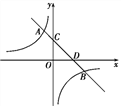
A. ①③ B. ①②④ C. ①③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,已知∠1=∠2,∠C=∠D

(1)判断BD与CE是否平行,并说明理由;(2)说明∠A=∠F的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=x-2与y轴交于点C,与x轴交于点B,与反比例函数y=
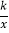 的图象在第一象限交于点A,连接OA,若S△AOB∶S△BOC=1∶2,则k的值为____.
的图象在第一象限交于点A,连接OA,若S△AOB∶S△BOC=1∶2,则k的值为____.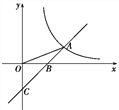
相关试题

