【题目】已知如图,已知∠1=∠2,∠C=∠D

(1)判断BD与CE是否平行,并说明理由;(2)说明∠A=∠F的理由.
参考答案:
【答案】(1)BD∥CE,见解析;(2)见解析.
【解析】
(1)根据对顶角和已知条件得∠1=∠3 ,再由平行线判定: 同位角相等,两直线平行即可解答.
(2)由平行线性质: 两直线平行,同位角相等得∠DBA=∠C,结合已知条件得∠DBA=∠D,再由平行线判定: 内错角相等,两直线平行得 DF∥AC ,根据平行线性质: 两直线平行,内错角相等即可解答.
(1)如图,
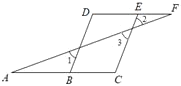
BD∥CE,理由如下:
∵∠1=∠2,∠2=∠3
∴∠1=∠3(等量代换),
∴BD∥CE(同位角相等,两直线平行)
(2)∵BD∥CE
∴∠DBA=∠C(两直线平行,同位角相等),
∵∠C=∠D,
∴∠DBA=∠D,
∴DF∥AC(内错角相等,两直线平行)
∴∠A=∠F(两直线平行,内错角相等)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.

(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明想测山高和索道的长度.他在B处仰望山顶A,测得仰角∠B=31°,再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=39°.

(1)求这座山的高度(小明的身高忽略不计);
(2)求索道AC的长(结果精确到0.1m).
(参考数据:tan31°≈ ,sin31°≈
,sin31°≈  ,tan39°≈
,tan39°≈  ,sin39°≈
,sin39°≈  )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强学生的安全意识,某校组织了学生参加安全知识竞赛,从中抽取了部分学生成绩(得分数取正整数,满分为100分)进行统计,绘制统计图如下(未完成),解答下列问题:


(1)若A组的频数比B组小24,求频数分布直方图中的
 、
、 的值;
的值;(2)扇形统计图中,D部分所对的圆心角为n°,求n的值并补全频数分布直方图;
(3)若成绩在80分以上为优秀,全校共有2000名学生,估计成绩优异的学生有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知平行四边形ABCD,延长AD到E,使DE=AD,连接BE与DC交于O点.

(1)求证:△BOC≌△EOD;
(2)当△ABE满足什么条件时,四边形BCED是菱形?证明你的结论. -
科目: 来源: 题型:
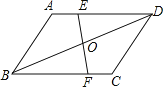
查看答案和解析>>【题目】已知:如图,在ABCD中,点E、F分别在AD、BC上,EF与BD相交于点O,AE=CF.
(1)求证:OE=OF;
(2)连接BE、DF,若BD平分∠EBF,试判断四边形EBFD的形状,并给予证明.
相关试题

