【题目】在如图所示的直角坐标系中,解答下列问题: 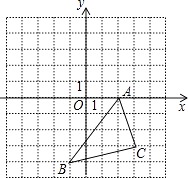
(1)分别写出A、B两点的坐标;
(2)将△ABC绕点A顺时针旋转90°,画出旋转后的△AB1C1;
(3)求出线段B1A所在直线l的函数解析式,并写出在直线l上从B1到A的自变量x的取值范围.
参考答案:
【答案】
(1)解:从图中可得出:
A(2,0),B(﹣1,﹣4)
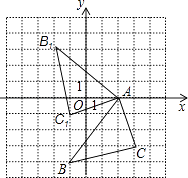
(2)解:画图

(3)解:设线段B1A所在直线l的解析式为:y=kx+b(k≠0),
∵B1(﹣2,3),A(2,0),
∴ ![]() ,
,
![]() ,
,
∴线段B1A所在直线l的解析式为: ![]() ,
,
线段B1A的自变量x的取值范围是:﹣2≤x≤2
【解析】(1)从直角坐标系中读出点的坐标.(2)让三角形的各顶点都绕点A顺时针旋转90°后得到对应点,顺次连接即可.(3)先设出一般的一次函数的解析式,再把点的坐标代入求解析式即可.
【考点精析】通过灵活运用确定一次函数的表达式,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程中变形正确的是( )
①3x+6=0变形为x+2=0;
②2x+8=5-3x变形为x=3;
③
 +
+ =4去分母,得3x+2x=24;
=4去分母,得3x+2x=24;④(x+2)-2(x-1)=0去括号,得x+2-2x-2=0.
A. ①③ B. ①②③ C. ①④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售“喜羊羊”玩具,预测该产品能够畅销,就用32000元购进了一批这种玩具,上市后很快脱销,商场又用68000元购进第二批这种玩具,所购数量是第一批购进数量的2倍,但每个进价多了10元.
(1)该商场两次共购进这种玩具多少个?
(2)如果这两批玩具每套的售价相同,且全部售完后总利润率不低于20%,那么每件售价至少是多少元?(利润率
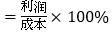 )
) -
科目: 来源: 题型:
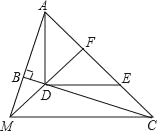
查看答案和解析>>【题目】如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD、AB的延长线相交于点M,连接MC.
(1)求证:∠FMC=∠FCM;
(2)将条件中的AD⊥DE与(1)中的结论互换,其他条件不变,命题是否正确?请给出理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,∠ABC=2∠C,BE平分∠ABC交AC于E,AD⊥BE于D,下列结论:①AC﹣BE=AE;②点E在线段BC的垂直平分线上;③∠DAE=∠C;④BC=4AD,其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣2(m+1)x+m(m+2)
(1)求证:无论m为任何实数,该函数图象与x轴两个交点之间的距离为定值.
(2)若该函数图象的对称轴为直线x=2,试求二次函数的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】以线段AC为对角线的四边形ABCD(它的四个顶点A,B,C,D按顺时针方向排列),已知AB=BC=CD,∠ABC=100°,∠CAD=40°,则∠BCD的度数为________.
相关试题

