【题目】小红和小明在研究一个数学问题:已知AB∥CD,AB和CD都不经过点E,探索∠E与∠A,∠C的数量关系. 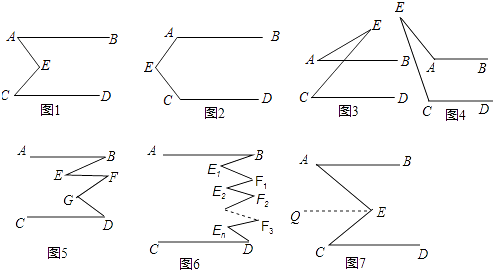
(1)发现:在图1中,小红和小明都发现:∠AEC=∠A+∠C; 小红是这样证明的:如图7过点E作EQ∥AB.
∴∠AEQ=∠A()
∵EQ∥AB,AB∥CD.
∴EQ∥CD()
∴∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C 即∠AEC=∠A+∠C.
小明是这样证明的:如图7过点E作EQ∥AB∥CD.
∴∠AEQ=∠A,∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C即∠AEC=∠A+∠C
请在上面证明过程的横线上,填写依据:
两人的证明过程中,完全正确的是 .
(2)尝试: ①在图2中,若∠A=110°,∠C=130°,则∠E的度数为;
②在图3中,若∠A=20°,∠C=50°,则∠E的度数为 .
(3)探索: 装置图4中,探索∠E与∠A,∠C的数量关系,并说明理由.
(4)猜想: 如图5,∠B、∠D、∠E、∠F、∠G之间有什么关系?(直接写出结论)
(5)如图6,你可以得到什么结论?(直接写出结论)
参考答案:
【答案】
(1)两直线平行,内错角相等;平行于同一直线的两直线平行;小红的证法
(2)120°;30°
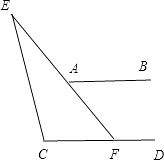
(3)解:∠E=∠A﹣∠C.
理由:延长EA,交CD于点F.
∵AB∥CD,
∴∠EFD=∠EAB
∵∠EFD=∠C+∠E
∴∠EAB=∠C+∠E
∴∠E=∠EAB﹣∠C.
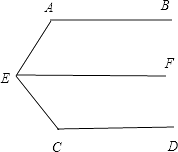
(4)解:可通过过点E、F、G分别做AB的平行线,得到结论.
∠E+∠G=∠B+∠F+∠D
(5)解:同上道理一样,可得到结论:∠E1+∠E2+…+∠En=∠F1+∠F2+…∠Fn﹣1+∠B+∠D.
【解析】解:(1.)∵小明的辅助线做不出来,所以两人的证明过程中,小红的完全正确;答案:两直线平行,内错角相等;平行于同一直线的两直线平行;小红的证法. (2.)①过点E作EF∥AB,
∵AB∥CD,
∴EF∥CD.∵EF∥AB,
∴∠A+∠AEF=180°,
∵∠A=110°,∴∠AEF=70°.
∵EF∥CD,
∴∠C+∠CEF=180°,
∵∠C=130°,∴∠CEF=50°.
②∵AB∥CD,
∴∠EOB=∠C=50°
∵∠EOB=∠A+∠E,
∵∠E=∠EOB﹣∠A=50°﹣20°=30°.
答案:120°,30°.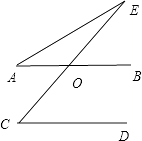
【考点精析】根据题目的已知条件,利用平行线的判定与性质的相关知识可以得到问题的答案,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线C:y=x2经过变化可得到抛物线C1:y1=a1x(x﹣b1),C1与x轴的正半轴交与点A1,且其对称轴分别交抛物线C,C1于点B1,D1,此时四边形OB1A1D1恰为正方形;按上述类似方法,如图2,抛物线C1:y1=a1x(x﹣b1)经过变换可得到抛物线C2:y2=a2x(x﹣b2),C2与x轴的正半轴交与点A2,且其对称轴分别交抛物线C1,C2于点B2,D2,此时四边形OB2A2D2也恰为正方形;按上述类似方法,如图3,可得到抛物线C3:y3=a3x(x﹣b3)与正方形OB3A3D3.请探究以下问题:
(1)填空:a1= ,b1= ;
(2)求出C2与C3的解析式;
(3)按上述类似方法,可得到抛物线Cn:yn=anx(x﹣bn)与正方形OBnAnDn(n≥1).
①请用含n的代数式直接表示出Cn的解析式;
②当x取任意不为0的实数时,试比较y2015与y2016的函数值的大小并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】平行公理的推论是如果两条直线都与 , 那么这两条直 线也 . 即三条直线a,b,c,若a∥b,b∥c,则 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个正多边形的内角和2340°,则边数为___.它的外角等于___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB是⊙O的直径,BC⊥CD于点C,AD⊥CD于点D,请仅用无刻度的直尺按下列要求作图.
(1)在图1中,当线段CD与⊙O相切时,请在CD上确定一点E,连接BE,使BE平分∠ABC;
(2)在图2中,当线段CD与⊙O相离时,请过点O作OF⊥CD,垂足为F.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应南充市创建“全国卫生城市”的号召,某校1500名学生参加了卫生知识竞赛,成绩记为A、B、C、D四等.从中随机抽取了部分学生成绩进行统计,绘制成如图两幅不完整的统计图表,根据图表信息,以下说法不正确的是( )
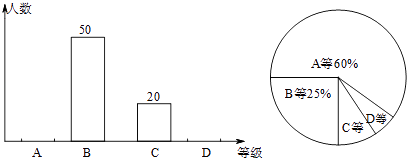
A.样本容量是200
B.D等所在扇形的圆心角为15°
C.样本中C等所占百分比是10%
D.估计全校学生成绩为A等大约有900人 -
科目: 来源: 题型:
查看答案和解析>>【题目】若方程 mx﹣2y=3x+4 是关于x、y 的二元一次方程,则 m 的取值范围是_____.
相关试题

