【题目】如图1,抛物线C:y=x2经过变化可得到抛物线C1:y1=a1x(x﹣b1),C1与x轴的正半轴交与点A1,且其对称轴分别交抛物线C,C1于点B1,D1,此时四边形OB1A1D1恰为正方形;按上述类似方法,如图2,抛物线C1:y1=a1x(x﹣b1)经过变换可得到抛物线C2:y2=a2x(x﹣b2),C2与x轴的正半轴交与点A2,且其对称轴分别交抛物线C1,C2于点B2,D2,此时四边形OB2A2D2也恰为正方形;按上述类似方法,如图3,可得到抛物线C3:y3=a3x(x﹣b3)与正方形OB3A3D3.请探究以下问题:
(1)填空:a1= ,b1= ;
(2)求出C2与C3的解析式;
(3)按上述类似方法,可得到抛物线Cn:yn=anx(x﹣bn)与正方形OBnAnDn(n≥1).
①请用含n的代数式直接表示出Cn的解析式;
②当x取任意不为0的实数时,试比较y2015与y2016的函数值的大小并说明理由.

参考答案:
【答案】(1)、1,2;(2)、y2=x(x﹣6);y3=x(x﹣14);(3)、yn=x2﹣(2n+1﹣2)x;当x<0时,y2015<y2016;当x>0时,y2015>y2016.
【解析】
试题分析:(1)、根据图形变换后二次项系数不变得出a1=1,代入抛物线C1解析式后,求与x轴交点A1坐标,根据正方形对角线性质表示出B1的坐标,代入对应的解析式即可求出对应的b1的值;(2)、根据图形变换后二次项系数不变得出a2=a1=1,代入抛物线C2解析式后,求与x轴交点A2坐标,根据正方形对角线性质表示出B2的坐标,代入对应的解析式即可求出对应的b2的值,写出抛物线C2的解析式;再利用相同的方法求抛物线C3的解析式;(3)、①根据图形变换后二次项系数不变得出an=a1=1,由B1坐标(1,1)、B2坐标(3,3)、B3坐标(7,7)得Bn坐标(2n﹣1,2n﹣1),则bn=2(2n﹣1)=2n+1﹣2(n≥1),写出抛物线Cn解析式.
②先求抛物线C2015和抛物线C2016的交点为(0,0),在交点的两侧观察图形得出y2015与y2016的函数值的大小.
试题解析:(1)、由抛物线C经过变换得到抛物线C1,则a1=1, 代入C1得:y1=x(x﹣b1),
y1=0时,x(x﹣b1)=0 x1=0,x2=b1 ∴A1(b1,0)
由正方形OB1A1D1得:OA1=B1D1=b1 ∴B1(![]() ,
,![]() )
)
∵B1在抛物线c上,则![]() =
=![]() b1(b1﹣2)=0 b1=0(不符合题意),b1=2
b1(b1﹣2)=0 b1=0(不符合题意),b1=2
(2)、由a2=a1=1得,y2=x(x﹣b2), y2=0时,x(x﹣b2)=0 x1=0,x2=b2 ∴A2(b2,0)
由正方形OB2A2D2得:OA2=B2D2=b2 ∴B2(![]() ,
,![]() ) ∵B2在抛物线c1上,则
) ∵B2在抛物线c1上,则![]() =(
=(![]() )2﹣2×
)2﹣2×![]() ,
,
b2(b2﹣6)=0 b2=0(不符合题意),b2=6 ∴C2的解析式:y2=x(x﹣6)=x2﹣6x,
由a3=a2=1得,y3=x(x﹣b3), y3=0时,x(x﹣b3)=0 x1=0,x2=b3 ∴A3(b3,0)
由正方形OB3A3D3得:OA3=B3D3=b3 ∴B3(![]() ,
,![]() ) ∵B3在抛物线c2上,则
) ∵B3在抛物线c2上,则![]() =(
=(![]() )2﹣6×
)2﹣6×![]() ,
,
b3(b3﹣14)=0 b3=0(不符合题意),b3=14 ∴C3的解析式:y3=x(x﹣14)=x2﹣14x,
(3)、①Cn的解析式:yn=x2﹣(2n+1﹣2)x(n≥1).
②由上题可得抛物线C2015的解析式为:y2015=x2﹣x=x2﹣x
抛物线C2016的解析式为:y2016=x2﹣x=x2﹣x
∴两抛物线的交点为(0,0);
∴当x<0时,y2015<y2016;当x>0时,y2015>y2016.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在抗击“新冠肺炎”时期,开展停课不停学活动,戴老师从3月1号到7号在网上答题个数记录如下
日期
1号
2号
3号
4号
5号
6号
7号
答题个数
68
55
50
56
54
48
68
在戴老师每天的答题个数所组成的这组数据中,众数和中位数依次是()
A.68,55B.55,68C.68,57D.55,57
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校食堂的中餐与晚餐的资费标准如下:
种类
单价
米饭
0.5元/份
A类套餐菜
3.5元/份
B类套餐菜
2.5元/份
小杰同学某星期从周一到周五每天的中餐与晚餐均在学校选用A类或B类中的一份套餐菜与一份米饭用餐,这五天共消费36元.请问小杰在这五天内,A,B类套餐菜各选用了多少次?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算结果正确的是( )
A.﹣2x2y3x3y3=﹣2x6y9B.12x6y4÷2x3y3=6x3y
C.3x3y2﹣x2y3=xyD.(﹣2a﹣3)(2a﹣3)=4a2﹣9
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行公理的推论是如果两条直线都与 , 那么这两条直 线也 . 即三条直线a,b,c,若a∥b,b∥c,则 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个正多边形的内角和2340°,则边数为___.它的外角等于___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红和小明在研究一个数学问题:已知AB∥CD,AB和CD都不经过点E,探索∠E与∠A,∠C的数量关系.
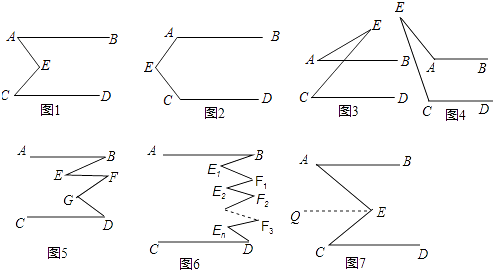
(1)发现:在图1中,小红和小明都发现:∠AEC=∠A+∠C; 小红是这样证明的:如图7过点E作EQ∥AB.
∴∠AEQ=∠A()
∵EQ∥AB,AB∥CD.
∴EQ∥CD()
∴∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C 即∠AEC=∠A+∠C.
小明是这样证明的:如图7过点E作EQ∥AB∥CD.
∴∠AEQ=∠A,∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C即∠AEC=∠A+∠C
请在上面证明过程的横线上,填写依据:
两人的证明过程中,完全正确的是 .
(2)尝试: ①在图2中,若∠A=110°,∠C=130°,则∠E的度数为;
②在图3中,若∠A=20°,∠C=50°,则∠E的度数为 .
(3)探索: 装置图4中,探索∠E与∠A,∠C的数量关系,并说明理由.
(4)猜想: 如图5,∠B、∠D、∠E、∠F、∠G之间有什么关系?(直接写出结论)
(5)如图6,你可以得到什么结论?(直接写出结论)
相关试题

