【题目】如图,线段AB是⊙O的直径,BC⊥CD于点C,AD⊥CD于点D,请仅用无刻度的直尺按下列要求作图.
(1)在图1中,当线段CD与⊙O相切时,请在CD上确定一点E,连接BE,使BE平分∠ABC;
(2)在图2中,当线段CD与⊙O相离时,请过点O作OF⊥CD,垂足为F.

参考答案:
【答案】(1)、答案见解析;(2)、答案见解析
【解析】
试题分析:(1)、构造矩形ADCM,对角相等交点为H,连接OH,延长OH交CD于E,连接BE,射线BE即为所求作;(2)、方法类似(1).
试题解析:(1)、如图1中,设BC交⊙O于M,连接AM、AC、DM,AC与DM交于点H,连接OH,延长OH交CD于点E,连接BE,BE即为所求作
(2)、如图2中,


设BC交⊙O于M,连接AM、AC、DM,AC与DM交于点H,连接OH,延长OH交CD于点F,则OF⊥CD于F
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行公理的推论是如果两条直线都与 , 那么这两条直 线也 . 即三条直线a,b,c,若a∥b,b∥c,则 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个正多边形的内角和2340°,则边数为___.它的外角等于___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红和小明在研究一个数学问题:已知AB∥CD,AB和CD都不经过点E,探索∠E与∠A,∠C的数量关系.
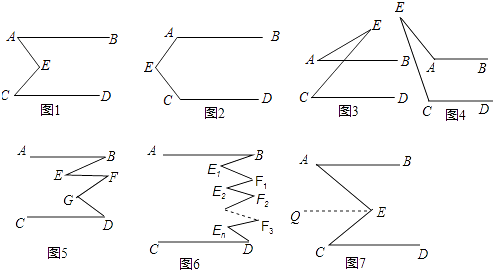
(1)发现:在图1中,小红和小明都发现:∠AEC=∠A+∠C; 小红是这样证明的:如图7过点E作EQ∥AB.
∴∠AEQ=∠A()
∵EQ∥AB,AB∥CD.
∴EQ∥CD()
∴∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C 即∠AEC=∠A+∠C.
小明是这样证明的:如图7过点E作EQ∥AB∥CD.
∴∠AEQ=∠A,∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C即∠AEC=∠A+∠C
请在上面证明过程的横线上,填写依据:
两人的证明过程中,完全正确的是 .
(2)尝试: ①在图2中,若∠A=110°,∠C=130°,则∠E的度数为;
②在图3中,若∠A=20°,∠C=50°,则∠E的度数为 .
(3)探索: 装置图4中,探索∠E与∠A,∠C的数量关系,并说明理由.
(4)猜想: 如图5,∠B、∠D、∠E、∠F、∠G之间有什么关系?(直接写出结论)
(5)如图6,你可以得到什么结论?(直接写出结论) -
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应南充市创建“全国卫生城市”的号召,某校1500名学生参加了卫生知识竞赛,成绩记为A、B、C、D四等.从中随机抽取了部分学生成绩进行统计,绘制成如图两幅不完整的统计图表,根据图表信息,以下说法不正确的是( )
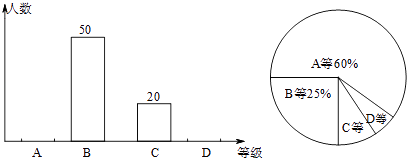
A.样本容量是200
B.D等所在扇形的圆心角为15°
C.样本中C等所占百分比是10%
D.估计全校学生成绩为A等大约有900人 -
科目: 来源: 题型:
查看答案和解析>>【题目】若方程 mx﹣2y=3x+4 是关于x、y 的二元一次方程,则 m 的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】过线段外一点画这条线段的垂线,垂足一定在( )
A.线段上
B.线段的端点上
C.线段的延长线上
D.以上情况都有可能
相关试题

