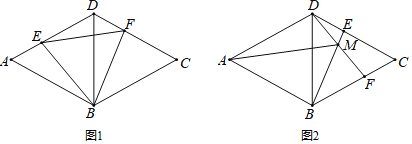
【题目】如图,已知菱形ABCD边长为4,![]() ,点E从点A出发沿着AD、DC方向运动,同时点F从点D出发以相同的速度沿着DC、CB的方向运动.
,点E从点A出发沿着AD、DC方向运动,同时点F从点D出发以相同的速度沿着DC、CB的方向运动.
![]() 如图1,当点E在AD上时,连接BE、BF,试探究BE与BF的数量关系,并证明你的结论;
如图1,当点E在AD上时,连接BE、BF,试探究BE与BF的数量关系,并证明你的结论;
![]() 在
在![]() 的前提下,求EF的最小值和此时
的前提下,求EF的最小值和此时![]() 的面积;
的面积;
![]() 当点E运动到DC边上时,如图2,连接BE、DF,交点为点M,连接AM,则
当点E运动到DC边上时,如图2,连接BE、DF,交点为点M,连接AM,则![]() 大小是否变化?请说明理由.
大小是否变化?请说明理由.
参考答案:
【答案】![]() ,证明见解析;
,证明见解析;![]() 的最小值是
的最小值是![]() ,
,![]() ;
;![]() 如图3,当点E运动到DC边上时,
如图3,当点E运动到DC边上时,![]() 大小不发生变化,理由见解析.
大小不发生变化,理由见解析.
【解析】
![]() 先证明
先证明![]() 和
和![]() 是等边三角形,再证明
是等边三角形,再证明![]() ≌
≌![]() ,可得结论;
,可得结论;
![]() 由
由![]() ≌
≌![]() ,易证得
,易证得![]() 是正三角形,继而可得当动点E运动到当
是正三角形,继而可得当动点E运动到当![]() ,即E为AD的中点时,BE的最小,根据等边三角形三线合一的性质可得BE和EF的长,并求此时
,即E为AD的中点时,BE的最小,根据等边三角形三线合一的性质可得BE和EF的长,并求此时![]() 的面积;
的面积;
![]() 同理得:
同理得:![]() ≌
≌![]() ,则可得
,则可得![]() ,所以
,所以![]() ,则A、B、M、D四点共圆,可得
,则A、B、M、D四点共圆,可得![]() .
.
![]() ,
,
证明:![]() 、F的速度相同,且同时运动,
、F的速度相同,且同时运动,
![]() ,
,
又![]() 四边形ABCD是菱形,
四边形ABCD是菱形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
同理![]() 也是等边三角形,
也是等边三角形,
![]() ,
,
在![]() 和
和![]() 中,
中,
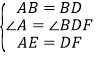 ,
,
![]() ≌
≌![]() ,
,
![]() ;
;
![]() 由
由![]() 得:
得:![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
如图2,当动点E运动到![]() ,即E为AD的中点时,BE的最小,此时EF最小,
,即E为AD的中点时,BE的最小,此时EF最小,
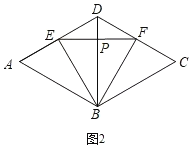
![]() ,
,![]() ,
,
![]() ,
,
![]() 的最小值是
的最小值是![]() ,
,
![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() 如图3,当点E运动到DC边上时,
如图3,当点E运动到DC边上时,![]() 大小不发生变化,
大小不发生变化,
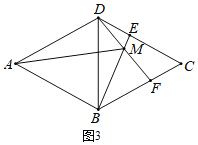
在![]() 和
和![]() 中,
中,
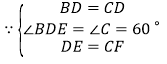 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 、B、M、D四点共圆,
、B、M、D四点共圆,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形OABC的顶点A的坐标为(3,4),顶点C在x轴的正半轴上,反比例函数y=
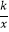 (x>0)的图象经过顶点B,则反比例函数的表达式为( )
(x>0)的图象经过顶点B,则反比例函数的表达式为( ) 
A.y=
B.y=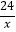
C.y=
D.y=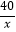
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题的提出:如果点P是锐角
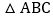 内一动点,如何确定一个位置,使点P到
内一动点,如何确定一个位置,使点P到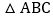 的三顶点的距离之和
的三顶点的距离之和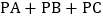 的值为最小?
的值为最小?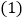 问题的转化:把
问题的转化:把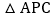 绕点A逆时针旋转
绕点A逆时针旋转 得到
得到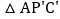 ,连接
,连接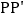 ,这样就把确定
,这样就把确定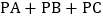 的最小值的问题转化成确定
的最小值的问题转化成确定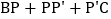 的最小值的问题了,请你利用图1证明:
的最小值的问题了,请你利用图1证明: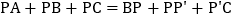 ;
;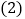 问题的解决:当点P到锐角
问题的解决:当点P到锐角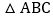 的三顶点的距离之和
的三顶点的距离之和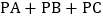 的值为最小时,求
的值为最小时,求 和
和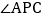 的度数;
的度数;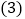 问题的延伸:如图2是有一个锐角为
问题的延伸:如图2是有一个锐角为 的直角三角形,如果斜边为2,点P是这个三角形内一动点,请你利用以上方法,求点P到这个三角形各顶点的距离之和的最小值.
的直角三角形,如果斜边为2,点P是这个三角形内一动点,请你利用以上方法,求点P到这个三角形各顶点的距离之和的最小值.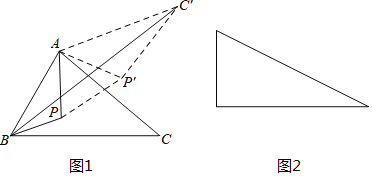
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac﹣b2<0;其中正确的结论有( )

A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大树AB与大数CD相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为90°,且EA=ED.已知大树AB的高为5m,小华行走的速度为1m/s,小华行走到点E的时间是( )

A. 13s B. 8s C. 6s D. 5s
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4),延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1…按这样的规律进行下去,第2018个正方形的面积为( )

A. 20×(
 )2017 B. 20×(
)2017 B. 20×( )2018 C. 20×(
)2018 C. 20×( )4036 D. 20×(
)4036 D. 20×( )4034
)4034 -
科目: 来源: 题型:
查看答案和解析>>【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费.为更好地决策,自来水公司的随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括在右端点但不包括左端点),请你根据统计图解答下列问题:

(1)此次抽样调查的样本容量是 .
(2)补全频数分布直方图,并求扇形图中“15吨~20吨”部分的圆心角的度数.
(3)如果自来水公司将基本用水量定位每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?
相关试题

