【题目】问题的提出:如果点P是锐角![]() 内一动点,如何确定一个位置,使点P到
内一动点,如何确定一个位置,使点P到![]() 的三顶点的距离之和
的三顶点的距离之和![]() 的值为最小?
的值为最小?
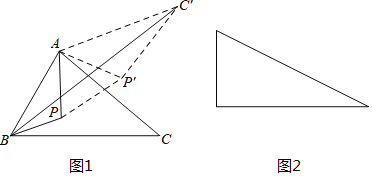
![]() 问题的转化:把
问题的转化:把![]() 绕点A逆时针旋转
绕点A逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,这样就把确定
,这样就把确定![]() 的最小值的问题转化成确定
的最小值的问题转化成确定![]() 的最小值的问题了,请你利用图1证明:
的最小值的问题了,请你利用图1证明:![]() ;
;
![]() 问题的解决:当点P到锐角
问题的解决:当点P到锐角![]() 的三顶点的距离之和
的三顶点的距离之和![]() 的值为最小时,求
的值为最小时,求![]() 和
和![]() 的度数;
的度数;
![]() 问题的延伸:如图2是有一个锐角为
问题的延伸:如图2是有一个锐角为![]() 的直角三角形,如果斜边为2,点P是这个三角形内一动点,请你利用以上方法,求点P到这个三角形各顶点的距离之和的最小值.
的直角三角形,如果斜边为2,点P是这个三角形内一动点,请你利用以上方法,求点P到这个三角形各顶点的距离之和的最小值.
参考答案:
【答案】(1)证明见解析;(2)满足:![]() 时,
时,![]() 的值为最小;(3)点P到这个三角形各顶点的距离之和的最小值为
的值为最小;(3)点P到这个三角形各顶点的距离之和的最小值为![]() .
.
【解析】
![]() 问题的转化:根据旋转的性质证明△APP是等边三角形,则PP=PA,可得结论;
问题的转化:根据旋转的性质证明△APP是等边三角形,则PP=PA,可得结论;
![]() 问题的解决:运用类比的思想,把
问题的解决:运用类比的思想,把![]() 绕点A逆时针旋转60度得到
绕点A逆时针旋转60度得到![]() ,连接
,连接![]() ,由“问题的转化”可知:当B、P、P、C在同一直线上时,
,由“问题的转化”可知:当B、P、P、C在同一直线上时,![]() 的值为最小,确定当:
的值为最小,确定当:![]() 时,满足三点共线;
时,满足三点共线;
![]() 问题的延伸:如图3,作辅助线,构建直角△ABC,利用勾股定理求AC的长,即是点P到这个三角形各顶点的距离之和的最小值.
问题的延伸:如图3,作辅助线,构建直角△ABC,利用勾股定理求AC的长,即是点P到这个三角形各顶点的距离之和的最小值.
问题的转化:
如图1,
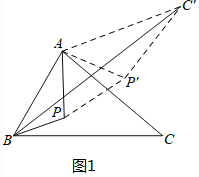
由旋转得:∠PAP=60°,PA=PA,
△APP是等边三角形,
∴PP=PA,
∵PC=PC,
![]() .
.
问题的解决:
满足:![]() 时,
时,![]() 的值为最小;
的值为最小;
理由是:如图2,把![]() 绕点A逆时针旋转60度得到
绕点A逆时针旋转60度得到![]() ,连接
,连接![]() ,
,
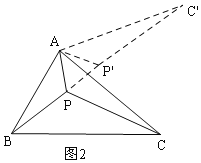
由“问题的转化”可知:当B、P、P、C在同一直线上时,![]() 的值为最小,
的值为最小,
![]() ,∠APP=60°,
,∠APP=60°,
∴∠APB+∠APP=180°,
![]() 、P、P在同一直线上,
、P、P在同一直线上,
由旋转得:∠APC=∠APC=120°,
∵∠APP=60°,
∴∠APC+∠A PP=180°,
![]() 、P、C在同一直线上,
、P、C在同一直线上,
![]() 、P、P、C在同一直线上,
、P、P、C在同一直线上,
![]() 此时
此时![]() 的值为最小,
的值为最小,
故答案为:![]() ;
;
问题的延伸:
如图3,![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
把![]() 绕点B逆时针旋转60度得到
绕点B逆时针旋转60度得到![]() ,连接
,连接![]() ,
,
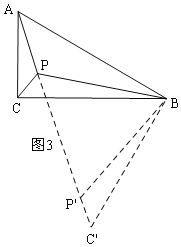
当A、P、P、C在同一直线上时,![]() 的值为最小,
的值为最小,
由旋转得:BP=BP,∠PBP=60°,PC=PC,BC=BC,
![]() 是等边三角形,
是等边三角形,
∴PP=PB,
∵∠ABC=∠APB+∠CBP=∠APB+∠CBP=30°,
∴∠ABC=90°,
由勾股定理得:AC=![]() ,
,
∴PA+PB+PC=PA+PP+PC=AC=![]() ,
,
则点P到这个三角形各顶点的距离之和的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,
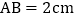 ,
,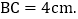 点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是
点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是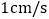 ,连接PQ、AQ、
,连接PQ、AQ、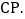 设点P、Q运动的时间为ts.
设点P、Q运动的时间为ts. 当t为何值时,四边形ABQP是矩形;
当t为何值时,四边形ABQP是矩形; 当t为何值时,四边形AQCP是菱形.
当t为何值时,四边形AQCP是菱形.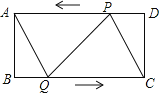
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长都为 a 的正方形内分别排列着一些大小相等的圆:
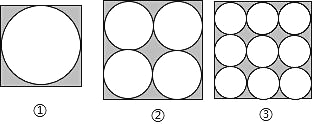
(1)根据图中的规律,第 4 个正方形内圆的个数是 ,第n 个正方形内圆的个数是_____.
(2)如果把正方形内除去圆的部分都涂上阴影.
①用含a 的代数式分别表示第 1 个正方形中、第 3 个正方形中阴影部分的面积(结果保留π);
②若 a=10,请直接写出第 2018 个正方形中阴影都分的面积 (结果保留π)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形OABC的顶点A的坐标为(3,4),顶点C在x轴的正半轴上,反比例函数y=
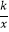 (x>0)的图象经过顶点B,则反比例函数的表达式为( )
(x>0)的图象经过顶点B,则反比例函数的表达式为( ) 
A.y=
B.y=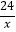
C.y=
D.y=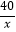
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac﹣b2<0;其中正确的结论有( )

A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD边长为4,
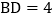 ,点E从点A出发沿着AD、DC方向运动,同时点F从点D出发以相同的速度沿着DC、CB的方向运动.
,点E从点A出发沿着AD、DC方向运动,同时点F从点D出发以相同的速度沿着DC、CB的方向运动. 如图1,当点E在AD上时,连接BE、BF,试探究BE与BF的数量关系,并证明你的结论;
如图1,当点E在AD上时,连接BE、BF,试探究BE与BF的数量关系,并证明你的结论; 在
在 的前提下,求EF的最小值和此时
的前提下,求EF的最小值和此时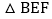 的面积;
的面积; 当点E运动到DC边上时,如图2,连接BE、DF,交点为点M,连接AM,则
当点E运动到DC边上时,如图2,连接BE、DF,交点为点M,连接AM,则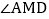 大小是否变化?请说明理由.
大小是否变化?请说明理由.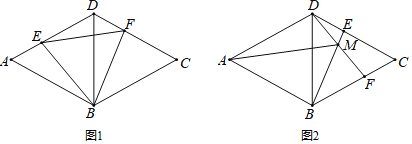
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大树AB与大数CD相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为90°,且EA=ED.已知大树AB的高为5m,小华行走的速度为1m/s,小华行走到点E的时间是( )

A. 13s B. 8s C. 6s D. 5s
相关试题

