【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费.为更好地决策,自来水公司的随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括在右端点但不包括左端点),请你根据统计图解答下列问题: 
(1)此次抽样调查的样本容量是 .
(2)补全频数分布直方图,并求扇形图中“15吨~20吨”部分的圆心角的度数.
(3)如果自来水公司将基本用水量定位每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?
参考答案:
【答案】
(1)100
(2)解:用水15~20吨的户数:100﹣10﹣36﹣24﹣8=22(户)
∴补充图如下:

“15吨~20吨”部分的圆心角的度数=360°× ![]() =79.2°
=79.2°
答:扇形图中“15吨~20吨”部分的圆心角的度数为79.2°
(3)解:6× ![]() =4.08(万户)
=4.08(万户)
答:该地区6万用户中约有4.08万用户的用水全部享受基本价格
【解析】解:(1)∵10÷10%=100(户) ∴样本容量是100,
故答案为:100;
(1)根据10~15吨部分的用户数和百分比进行计算;(2)先根据频数分布直方图中的数据,求得“15吨~20吨”部分的用户数,再画图,最后根据该部分的用户数计算圆心角的度数;(3)根据用水25吨以内的用户数的占比,求得该地区6万用户中用水全部享受基本价格的户数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD边长为4,
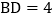 ,点E从点A出发沿着AD、DC方向运动,同时点F从点D出发以相同的速度沿着DC、CB的方向运动.
,点E从点A出发沿着AD、DC方向运动,同时点F从点D出发以相同的速度沿着DC、CB的方向运动. 如图1,当点E在AD上时,连接BE、BF,试探究BE与BF的数量关系,并证明你的结论;
如图1,当点E在AD上时,连接BE、BF,试探究BE与BF的数量关系,并证明你的结论; 在
在 的前提下,求EF的最小值和此时
的前提下,求EF的最小值和此时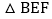 的面积;
的面积;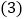 当点E运动到DC边上时,如图2,连接BE、DF,交点为点M,连接AM,则
当点E运动到DC边上时,如图2,连接BE、DF,交点为点M,连接AM,则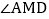 大小是否变化?请说明理由.
大小是否变化?请说明理由.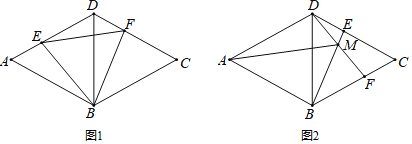
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大树AB与大数CD相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为90°,且EA=ED.已知大树AB的高为5m,小华行走的速度为1m/s,小华行走到点E的时间是( )

A. 13s B. 8s C. 6s D. 5s
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4),延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1…按这样的规律进行下去,第2018个正方形的面积为( )

A. 20×(
 )2017 B. 20×(
)2017 B. 20×( )2018 C. 20×(
)2018 C. 20×( )4036 D. 20×(
)4036 D. 20×( )4034
)4034 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上三点M,O,N对应的数分别为-1,0,3,点P为数轴上任意一点,其对应的数为x.

(1)MN的长为 ;
(2)如果点P到点M、点N的距离相等,那么x的值是 ;
(3)数轴上是否存在点P,使点P到点M、点N的距离之和是8?若存在,直接写出x的值;若不存在,请说明理由.
(4)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+
 )海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
)海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OP平分∠BOA,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论中错误的是( )

A. PC=PD B. OC=OD C. OC=OP D. ∠CPO=∠DPO
相关试题

