【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,2),则点B2018的坐标为_____.
,0),B(0,2),则点B2018的坐标为_____.

参考答案:
【答案】(6054,2)
【解析】分析:
分析题意和图形可知,点B1、B3、B5、……在x轴上,点B2、B4、B6、……在第一象限内,由已知易得AB=![]() ,结合旋转的性质可得OA+AB1+B1C2=6,从而可得点B2的坐标为(6,2),同理可得点B4的坐标为(12,2),即点B2相当于是由点B向右平移6个单位得到的,点B4相当于是由点B2向右平移6个单位得到的,由此即可推导得到点B2018的坐标.
,结合旋转的性质可得OA+AB1+B1C2=6,从而可得点B2的坐标为(6,2),同理可得点B4的坐标为(12,2),即点B2相当于是由点B向右平移6个单位得到的,点B4相当于是由点B2向右平移6个单位得到的,由此即可推导得到点B2018的坐标.
详解:
∵在△AOB中,∠AOB=90°,OA=![]() ,OB=2,
,OB=2,
∴AB=![]() ,
,
∴由旋转的性质可得:OA+AB1+B1C2=OA+AB+OB=6,C2B2=OB=2,
∴点B2的坐标为(6,2),
同理可得点B4的坐标为(12,2),
由此可得点B2相当于是由点B向右平移6个单位得到的,点B4相当于是由点B2向右平移6个单位得到,
∴点B2018相当于是由点B向右平移了:![]() 个单位得到的,
个单位得到的,
∴点B2018的坐标为(6054,2).
故答案为:(6054,2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】盒中有x个黑球和y个白球,这些球除颜色外无其他差别.若从盒中随机取一个球,它是黑球的概率是
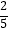 ;若往盒中再放进1个黑球,这时取得黑球的概率变为
;若往盒中再放进1个黑球,这时取得黑球的概率变为  .
.
(1)填空:x= , y=;
(2)小王和小林利用x个黑球和y个白球进行摸球游戏.约定:从盒中随机摸取一个,接着从剩下的球中再随机摸取一个,若两球颜色相同则小王胜,若颜色不同则小林胜.求两个人获胜的概率各是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图在四边形ABCD中,∠A=90°,AD=6,AB=8,BC=26,CD=24
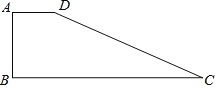
(1)求四边形ABCD的面积.
(2)求D到BC的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠A,∠B,∠C的对边分别记为
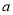 ,
, ,
,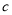 ,由下列条件不能判定△ABC为直角三角形的是( ).
,由下列条件不能判定△ABC为直角三角形的是( ).A.∠A+∠B=∠C
B.∠A∶∠B∶∠C =1∶2∶3
C.

D.
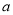 ∶
∶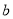 ∶
∶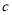 =3∶4∶6
=3∶4∶6 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,四边形
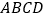 中,
中,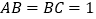 ,
,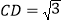 ,
,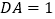 ,且
,且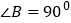 ,
,试求:(1)
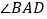 的度数;(2)四边形
的度数;(2)四边形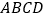 的面积(结果保留根号);
的面积(结果保留根号);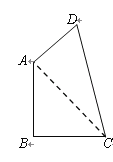
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点就做格点,以格点为顶点分别按下列要求画三角形;
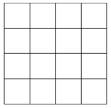
(1)使三角形的三边长分别为2,3,
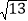
(在图中画出一个既可);
(2)请在数轴上作出
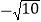 的对应点
的对应点
(2)如图①,A,B,C是三个格点(即小正方形的顶点),判断AB与BC的位置关系,并说明理由;
(3)如图②,连接三格和两格的对角线,求∠α+∠β的度数(要求:画出示意图,并说明理由).


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,底面积为30cm2的空圆柱形容器内水平放置着由两个实心圆柱组成的“几何体”,现向容器内匀速注水,注满为止,在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图②所示.
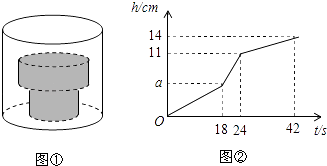
请根据图中提供的信息,解答下列问题:
(1)圆柱形容器的高为cm,匀速注水的水流速度为cm3/s;
(2)若“几何体”的下方圆柱的底面积为15cm2 , 求“几何体”上方圆柱的高和底面积.
相关试题

