【题目】已知,如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,
试求:(1)![]() 的度数;(2)四边形
的度数;(2)四边形![]() 的面积(结果保留根号);
的面积(结果保留根号);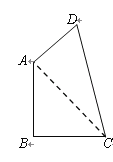
参考答案:
【答案】(1)![]() ;
;
(2)![]()
【解析】
(1)连接AC,由勾股定理求出AC的长,再根据勾股定理的逆定理判断出△ACD的形状,进而可求出∠BAD的度数;
(2)由(1)可知△ABC和△ADC是Rt△,再根据S四边形ABCD=S△ABC+S△ADC即可得出结论.
解:(1)连接AC,如图所示:
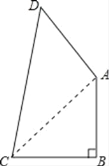
∵AB=BC=1,∠B=90°
∴AC=![]() ,
,
又∵AD=1,DC=![]() ,
,
∴ AD2+AC2=3 CD2=(![]() )2=3
)2=3
即CD2=AD2+AC2
∴∠DAC=90°
∵AB=BC=1
∴∠BAC=∠BCA=45°
∴∠BAD=135°;
(2)由(1)可知△ABC和△ADC是Rt△,
∴S四边形ABCD=S△ABC+S△ADC=1×1×![]() +1×
+1×![]() ×
×![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在四边形ABCD中,∠A=90°,AD=6,AB=8,BC=26,CD=24
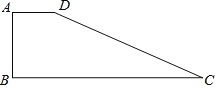
(1)求四边形ABCD的面积.
(2)求D到BC的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠A,∠B,∠C的对边分别记为
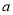 ,
, ,
,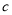 ,由下列条件不能判定△ABC为直角三角形的是( ).
,由下列条件不能判定△ABC为直角三角形的是( ).A.∠A+∠B=∠C
B.∠A∶∠B∶∠C =1∶2∶3
C.

D.
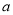 ∶
∶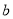 ∶
∶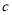 =3∶4∶6
=3∶4∶6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(
 ,0),B(0,2),则点B2018的坐标为_____.
,0),B(0,2),则点B2018的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点就做格点,以格点为顶点分别按下列要求画三角形;
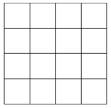
(1)使三角形的三边长分别为2,3,
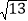
(在图中画出一个既可);
(2)请在数轴上作出
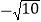 的对应点
的对应点
(2)如图①,A,B,C是三个格点(即小正方形的顶点),判断AB与BC的位置关系,并说明理由;
(3)如图②,连接三格和两格的对角线,求∠α+∠β的度数(要求:画出示意图,并说明理由).


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,底面积为30cm2的空圆柱形容器内水平放置着由两个实心圆柱组成的“几何体”,现向容器内匀速注水,注满为止,在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图②所示.
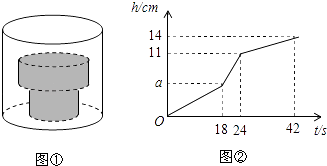
请根据图中提供的信息,解答下列问题:
(1)圆柱形容器的高为cm,匀速注水的水流速度为cm3/s;
(2)若“几何体”的下方圆柱的底面积为15cm2 , 求“几何体”上方圆柱的高和底面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形AEFG∽菱形ABCD,连接EB,GD.
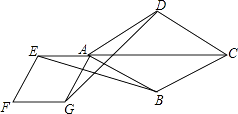
(1)求证:EB=GD;
(2)若∠DAB=60°,AB=2,AG=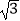 ,求GD的长.
,求GD的长.
相关试题

