搜索
【题目】用配方法解方程x2+10x+9=0，配方后可得（ ）
A.（x+5）2=16
B.（x+5）2=1
C.（x+10）2=91
D.（x+10）2=109
参考答案：
【答案】A
【解析】解：方程x2+10x+9=0，
整理得：x2+10x=﹣9，
配方得：x2+10x+25=16，即（x+5）2=16，
故选：A．
【考点精析】本题主要考查了配方法的相关知识点，需要掌握左未右已先分离，二系化“1”是其次．一系折半再平方，两边同加没问题．左边分解右合并，直接开方去解题才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们规定：三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差．如图1，在△ABC中，AO是BC边上的中线，AB与AC的“极化值”就等于AO2﹣BO2的值，可记为AB△AC=AO2﹣BO2 ．
（1）在图1中，若∠BAC=90°，AB=8，AC=6，AO是BC边上的中线，则AB△AC= ， OC△OA=；
（2）如图2，在△ABC中，AB=AC=4，∠BAC=120°，求AB△AC、BA△BC的值；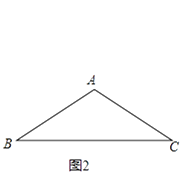
（3）如图3，在△ABC中，AB=AC，AO是BC边上的中线，点N在AO上，且ON=
AO．已知AB△AC=14，BN△BA=10，求△ABC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知a2+a﹣3=0，那么a2（a+4）的值是
-
科目： 来源： 题型：
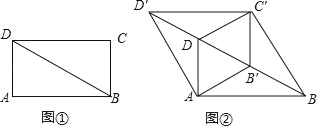
查看答案和解析>>【题目】如图①，BD是矩形ABCD的对角线，∠ABD=30°，AD=1．将△BCD沿射线BD方向平移到△B'C'D'的位置，使B'为BD中点，连接AB'，C'D，AD'，BC'，如图②．
（1）求证：四边形AB'C'D是菱形；
（2）四边形ABC'D′的周长为 ；
（3）将四边形ABC'D'沿它的两条对角线剪开，用得到的四个三角形拼成与其面积相等的矩形，直接写出所有可能拼成的矩形周长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】当a＝0时，方程ax+b＝0（其中x是未知数，b是已知数）的解的情况是（ ）
A. 唯一解B. 无解C. 有无数多个解D. 无解或有无数多个解
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在等腰三角形ABC中，∠BAC=120°，AB=AC=2，点D是BC边上的一个动点（不与B、C重合），在AC上取一点E，使∠ADE=30°．
（1）求证：△ABD∽△DCE；
（2）设BD=x，AE=y，求y关于x的函数关系式并写出自变量x的取值范围；
（3）当△ADE是等腰三角形时，求AE的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，将点A（x，y）向左平移5个单位长度，再向上平移3个单位长度后与点B（﹣3，2）重合，则点A的坐标是（ ）
A.（2，5）
B.（﹣8，5）
C.（﹣8，﹣1）
D.（2，﹣1）
相关试题
