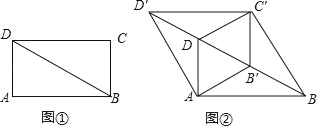
【题目】如图①,BD是矩形ABCD的对角线,∠ABD=30°,AD=1.将△BCD沿射线BD方向平移到△B'C'D'的位置,使B'为BD中点,连接AB',C'D,AD',BC',如图②.
(1)求证:四边形AB'C'D是菱形;
(2)四边形ABC'D′的周长为 ;
(3)将四边形ABC'D'沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.
参考答案:
【答案】(1)证明见解析;(2)4![]() ;(3)矩形周长为6+
;(3)矩形周长为6+![]() 或2
或2![]() +3.
+3.
【解析】试题分析:(1)有一组邻边相等的平行四边形是菱形,据此进行证明即可;
(2)先判定四边形ABC'D'是菱形,再根据边长AB=![]() AD=
AD=![]() ,即可得到四边形ABC'D′的周长为4
,即可得到四边形ABC'D′的周长为4![]() ;
;
(3)根据两种不同的拼法,分别求得可能拼成的矩形周长.
试题解析:(1)∵BD是矩形ABCD的对角线,∠ABD=30°,
∴∠ADB=60°,
由平移可得,B'C'=BC=AD,∠D'B'C'=∠DBC=∠ADB=60°,
∴AD∥B'C'
∴四边形AB'C'D是平行四边形,
∵B'为BD中点,
∴Rt△ABD中,AB'=![]() BD=DB',
BD=DB',
又∵∠ADB=60°,
∴△ADB'是等边三角形,
∴AD=AB',
∴四边形AB'C'D是菱形;
(2)由平移可得,AB=C'D',∠ABD'=∠C'D'B=30°,
∴AB∥C'D',
∴四边形ABC'D'是平行四边形,
由(1)可得,AC'⊥B'D,
∴四边形ABC'D'是菱形,
∵AB=![]() AD=
AD=![]() ,
,
∴四边形ABC'D′的周长为4![]() ,
,
故答案为:4![]() ;
;
(3)将四边形ABC'D'沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形如下:
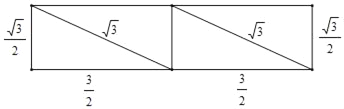
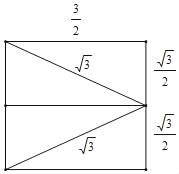
∴矩形周长为6+![]() 或2
或2![]() +3.
+3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F.

(1)若CE=8,CF=6,求OC的长;
(2)连接AE、AF.问:当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定:三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差.如图1,在△ABC中,AO是BC边上的中线,AB与AC的“极化值”就等于AO2﹣BO2的值,可记为AB△AC=AO2﹣BO2 .
(1)在图1中,若∠BAC=90°,AB=8,AC=6,AO是BC边上的中线,则AB△AC= , OC△OA=;
(2)如图2,在△ABC中,AB=AC=4,∠BAC=120°,求AB△AC、BA△BC的值;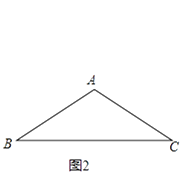
(3)如图3,在△ABC中,AB=AC,AO是BC边上的中线,点N在AO上,且ON= AO.已知AB△AC=14,BN△BA=10,求△ABC的面积.
AO.已知AB△AC=14,BN△BA=10,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2+a﹣3=0,那么a2(a+4)的值是
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解方程x2+10x+9=0,配方后可得( )
A.(x+5)2=16
B.(x+5)2=1
C.(x+10)2=91
D.(x+10)2=109 -
科目: 来源: 题型:
查看答案和解析>>【题目】当a=0时,方程ax+b=0(其中x是未知数,b是已知数)的解的情况是( )
A. 唯一解B. 无解C. 有无数多个解D. 无解或有无数多个解
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.

(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长.
相关试题

