【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,将
上,将![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在点
落在点![]() 处,当
处,当![]() 时,
时,![]() ________.
________.

参考答案:
【答案】![]() 或
或![]()
【解析】
分两种情况进行讨论:①当![]() 在
在![]() 上方时,由折叠可得
上方时,由折叠可得![]() ,当
,当![]() 时,
时,![]() ,再过点
,再过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() 是等腰三角形,再根据
是等腰三角形,再根据![]() 、
、![]() 是
是![]() 的中点、
的中点、![]() 求得
求得![]() 、
、![]() ,最后根据等腰
,最后根据等腰![]() 中,
中,![]() ,即可得到结论;②当
,即可得到结论;②当![]() 在
在![]() 下方时,同样是作辅助线构造等腰直角三角形和矩形,利用勾股定理进行计算求解.
下方时,同样是作辅助线构造等腰直角三角形和矩形,利用勾股定理进行计算求解.
解:①当![]() 在
在![]() 上方时
上方时
∵在![]() 中,
中,![]() ,
,![]() ,
,![]()
∴![]()
∵由折叠可得![]()
∴当![]() 时,
时,![]()
过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,如图:
,如图:
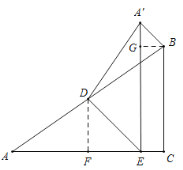
∴![]() 是等腰直角三角形
是等腰直角三角形
∵![]() 、
、![]() 是
是![]() 的中点、
的中点、![]()
∴![]() ,
,![]()
∴![]() ,
,![]()
∴矩形![]() 中,
中,![]() ,
,![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴等腰![]() 中,
中,![]() ;
;
②当![]() 在
在![]() 下方时
下方时
∵由折叠可得![]()
∴当![]() 时,
时,![]() ,
,![]()
∴![]()
过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,如图:
,如图:
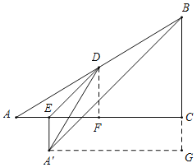
∴![]() 是等腰直角三角形
是等腰直角三角形
∴![]()
∵![]()
∴![]() ,
,![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴等腰![]() 中,
中,![]() .
.
∴综上所述,![]() 或
或![]() .
.
故答案是:![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形
 中,
中, 的平分线交
的平分线交 于点
于点 ,交
,交 的延长线于点
的延长线于点 ,
,
(1)写出
 对由条件
对由条件 推出的相等或互补的角
推出的相等或互补的角(2)
 与
与 相等吗?为什么?
相等吗?为什么?(3)证明:

请在下面的括号内,填上推理的根据,并完成下面的证明:
 ( ① )
( ① ) (已证),
(已证), ,( ② )
,( ② )又
 (角平分线的定义)
(角平分线的定义) ( ③ )
( ③ )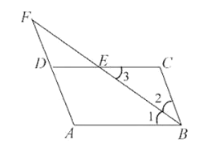
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
(1)求证:△ABF∽△BEC;
(2)若AD=5,AB=8,sinD=
 ,求AF的长.
,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=
 图象的两个交点.
图象的两个交点.(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣
 >0的解集.
>0的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有A、B、C、D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A、D两点表示的数分别为﹣5和6,且AC的中点为E,BD的中点为M,BC之间距点B的距离为
 BC的点N,则该数轴的原点为( )
BC的点N,则该数轴的原点为( )
A. 点E B. 点F C. 点M D. 点N
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,点
 是第一象限内的点,直线
是第一象限内的点,直线 与
与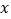 轴交于点
轴交于点 ,过点
,过点 作
作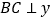 轴,垂足为
轴,垂足为 ,过点
,过点 的直线与
的直线与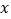 轴交于点
轴交于点 ,已知直线
,已知直线 上的点的坐标
上的点的坐标 是方程的
是方程的 解,直线
解,直线 上的点的坐标
上的点的坐标 是方程
是方程 的解
的解(1)求点
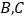 的坐标
的坐标(2)证明:
 (要求写出每一步的推理依据);
(要求写出每一步的推理依据);(3)求点
 的坐标,并求三角形
的坐标,并求三角形 的面积
的面积
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=90°,OC为一条射线,OE,OF分别平分∠AOC,∠BOC,那么∠EOF 的度数为_____________.
相关试题

