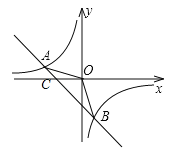
【题目】已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=![]() 图象的两个交点.
图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣![]() >0的解集.
>0的解集.

参考答案:
【答案】(1)反比例函数解析式为y=﹣![]() ,一次函数的解析式为y=﹣x﹣2;(2)6;(3)x<﹣4或0<x<2.
,一次函数的解析式为y=﹣x﹣2;(2)6;(3)x<﹣4或0<x<2.
【解析】试题分析:(1)先把点A的坐标代入反比例函数解析式,即可得到m=﹣8,再把点B的坐标代入反比例函数解析式,即可求出n=2,然后利用待定系数法确定一次函数的解析式;
(2)先求出直线y=﹣x﹣2与x轴交点C的坐标,然后利用S△AOB=S△AOC+S△BOC进行计算;
(3)观察函数图象得到当x<﹣4或0<x<2时,一次函数的图象在反比例函数图象上方,据此可得不等式的解集.
试题解析:(1)把A(﹣4,2)代入![]() ,得m=2×(﹣4)=﹣8,所以反比例函数解析式为
,得m=2×(﹣4)=﹣8,所以反比例函数解析式为![]() ,把B(n,﹣4)代入
,把B(n,﹣4)代入![]() ,得﹣4n=﹣8,解得n=2,把A(﹣4,2)和B(2,﹣4)代入y=kx+b,得:
,得﹣4n=﹣8,解得n=2,把A(﹣4,2)和B(2,﹣4)代入y=kx+b,得:![]() ,解得:
,解得:![]() ,所以一次函数的解析式为y=﹣x﹣2;
,所以一次函数的解析式为y=﹣x﹣2;
(2)y=﹣x﹣2中,令y=0,则x=﹣2,即直线y=﹣x﹣2与x轴交于点C(﹣2,0),∴S△AOB=S△AOC+S△BOC=![]() ×2×2+
×2×2+![]() ×2×4=6;
×2×4=6;
(3)由图可得,不等式![]() 的解集为:x<﹣4或0<x<2.
的解集为:x<﹣4或0<x<2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a3+a3=a6
B.(a2)3=a5
C.a2a3=a5
D.a6÷a3=a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】数据1,1,2,2,3,3,3 的极差是( )
A. 1 B. 2 C. 3 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次射击比赛中,甲、乙两名运动员10次射击的平均成绩都是7环,其中甲的成绩的方差S甲2=1.21,乙的成绩的方差S乙2=3.98,由此可知( ).
A. 甲比乙的成绩稳定 B. 乙比甲的成绩稳定
C. 甲、乙两人的成绩一样稳定 D. 无法确定谁的成绩更稳定
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式x3+2x2﹣3的常数项是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图, AD=CD=CB=AB=a,DA∥CB,AB⊥CB,∠BAC的平分线交BC于E,作EF⊥AC于F,作FG⊥AB于G.
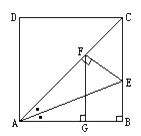
(1)求AC的长;
(2)求证:AB=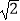 AG.
AG. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了丰富学生的校园生活,准备购进一批篮球和足球.其中篮球的单价比足球的单价多40元,用1500元购进的篮球个数与900元购进的足球个数相等.
(1)篮球和足球的单价各是多少元?
(2)该校打算用1000元购买篮球和足球,问恰好用完1000元,并且篮球、足球都买有的购买方案有哪几种?
相关试题

