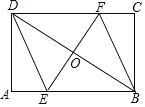
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
参考答案:
【答案】(1)证明见解析.(2)![]() .
.
【解析】
试题分析:(1)根据平行四边形ABCD的性质,判定△BOE≌△DOF(ASA),得出四边形BEDF的对角线互相平分,进而得出结论;
(2)在Rt△ADE中,由勾股定理得出方程,解方程求出BE,由勾股定理求出BD,得出OB,再由勾股定理求出EO,即可得出EF的长.
试题解析:(1)证明:∵四边形ABCD是矩形,O是BD的中点,
∴∠A=90°,AD=BC=4,AB∥DC,OB=OD,
∴∠OBE=∠ODF,
在△BOE和△DOF中,
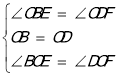 ,
,
∴△BOE≌△DOF(ASA),
∴EO=FO,
∴四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,BE⊥EF,
设BE=x,则 DE=x,AE=6﹣x,
在Rt△ADE中,DE2=AD2+AE2,
∴x2=42+(6﹣x)2,
解得:x=![]() ,
,
∵BD=![]() ,
,
∴OB=![]() BD=
BD=![]() ,
,
∵BD⊥EF,
∴EO=![]() ,
,
∴EF=2EO=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的三条线段能组成三角形的是( )
A.5cm2cm3cmB.5cm2cm2cm C.5cm2cm4cm D.5cm12cm6cm
-
科目: 来源: 题型:
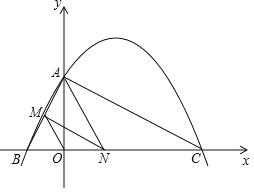
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】北京时间2019年4月10日21时,人类首张黑洞照片面世,该黑洞位于室女座一个巨椭圈星系M87的中心,距离地球55 000 000光年,其中数据55 000 000科学记数法表示为( )
A.55×106B.5.5×106C.5.5×107D.0.55×108
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点(a,1)与(﹣2,b)关于原点对称,则a+b=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不能判定两个三角形全等的条件是( )
A.三条边对应相等B.两条边及其夹角对应相等
C.两角及其中一角的对边对应相等D.两条边和一条边所对的角对应相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】全等图形是指两个图形( )
A.能够重合B.形状相同C.大小相同D.相等
相关试题

