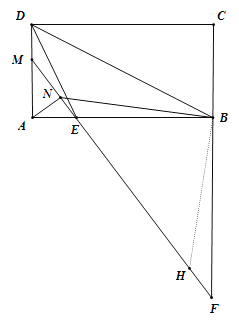
【题目】如图,四边形ABCD为矩形,连接BD,AB=2AD,点E在AB边上,连接ED.
(1)若∠ADE=30°,DE=6,求△BDE的面积;
(2)延长CB至点F使得BF=2AD,连接FE并延长交AD于点M,过点A作AN⊥EM于点N,连接BN,求证:FN=AN+![]() BN.
BN.

参考答案:
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)在Rt△ADE中,解直角三角形求出EA,DA的值,然后根据AB=2AD求出AB的长,进而求出BE的长,利用三角形的面积公式即可求出面积;
(2)作辅助线,构建全等三角形,证明△FHB≌△ANB,得BH=BN,HF=AN,则△HBN是等腰直角三角形,有NH=![]() NB,根据线段的和代入得结论.
NB,根据线段的和代入得结论.
试题解析:
解:(1)在Rt△ADE中,
∵∠EDA=30°,∴EA= ![]() ED=
ED= ![]() ×6=3,
×6=3,
DA=EDcos30°=6×![]() =3
=3![]() ,
,
∴BE=2DA﹣EA=6![]() ﹣3,∴S△BED=
﹣3,∴S△BED= ![]() ×BE×DA=
×BE×DA= ![]() (6
(6![]() ﹣3)×3
﹣3)×3![]() =
= ![]() ;
;
(2)如图,过B作BH⊥BN,交FM于H,
∴∠NBH=∠NBA+∠EBH=90°,
又∵∠ABF=∠HBF+∠EBH=90°,
∴∠NBA=∠HBF,
∵CF∥AD,
∴∠AMN=∠F,
∵AN⊥EM,
∴∠AMN+∠MAN=90°,
∠MAN+∠NAB=90°,
∴∠NAB=∠AMN,
∴∠NAB=∠F,
又∵BF=2AD,AB=2AD,
∴AB=BF,
∴△ANB≌△FHB,
∴BN=BH,AN=FH,
∴△BNH是等腰直角三角形,
∴NH=![]() NB,
NB,
∵FN=FH+NH
=AN+![]() NB/span>.
NB/span>.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点A(a,0),B(b,3),C(4,0),且满足
 +(a﹣b+6)2=0,线段AB交y轴于点F,点D是y轴正半轴上的一点.
+(a﹣b+6)2=0,线段AB交y轴于点F,点D是y轴正半轴上的一点.(1)求出点A,B的坐标;
(2)如图2,若DB∥AC,∠BAC=a,且AM,DM分别平分∠CAB,∠ODB,求∠AMD的度数;(用含a的代数式表示).
(3)如图3,坐标轴上是否存在一点P,使得△ABP的面积和△ABC的面积相等?若存在,求出P点坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一个长方形操场的四角都设计一块半径相同的四分之一圆形的花坛,若圆形的半径为r米,广场的长为a米,宽为b米.
(1)请列式表示操场空地的面积;
(2)若休闲广场的长为 50米,宽为20米,圆形花坛的半径为 3米,求操场空地的面积.(π取 3.14,计算结果保留 0.1)

-
科目: 来源: 题型:
查看答案和解析>>【题目】根据数轴和绝对值的知识回答下列问题

(1)一般地,数轴上表示数m和数n两点之间的距离我们可用│m-n│表示。
例如,数轴上4和1两点之间的距离是________.数轴上-3和2两点之间的距离是________.
(2) 数轴上表示数a的点位于-4与2之间,则│a+4│+│a-2│的值为_____________.
(3) 当a为何值时,│a+5│+│a-1│+│a-4│有最小值?最小值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个正方形内两个相邻正方形的面积分别为 4 和 2,它们都有两个顶点在大正方形的边 上且组成的图形为轴对称图形,则图中阴影部分的面积为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
关于
 的方程:
的方程: 的解为:
的解为:  ,
, 
 (可变形为
(可变形为 )的解为:
)的解为:  ,
, 
 的解为:
的解为:  ,
, 
 的解为:
的解为:  ,
, 
…………
根据以上材料解答下列问题:
(1)①方程
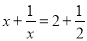 的解为 .
的解为 .②方程
 的解为 .
的解为 .(2)解关于
 方程:
方程:①
 (
( )
)②
 (
( )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于
 MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D. 下列结论:①AD是∠BAC的平分线;②点D在AB的垂直平分线上;③∠ADC=60°;④
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D. 下列结论:①AD是∠BAC的平分线;②点D在AB的垂直平分线上;③∠ADC=60°;④ 。其中正确的结论有( )
。其中正确的结论有( )
A. 1B. 2C. 3D. 4
相关试题

