Question

【题目】如图，二次函数y=﹣x2+3x+m的图象与x轴的一个交点为B（4，0），另一个交点为A，且与y轴相交于C点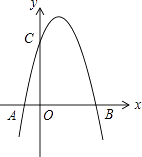

（1）求m的值及C点坐标；
（2）在直线BC上方的抛物线上是否存在一点M，使得它与B，C两点构成的三角形面积最大，若存在，求出此时M点坐标；若不存在，请简要说明理由
（3）P为抛物线上一点，它关于直线BC的对称点为Q
①当四边形PBQC为菱形时，求点P的坐标；
②点P的横坐标为t（0＜t＜4），当t为何值时，四边形PBQC的面积最大，请说明理由．

Answer 1

【答案】
（1）

解：将B（4，0）代入y=﹣x2+3x+m，

解得，m=4，

∴二次函数解析式为y=﹣x2+3x+4，

令x=0，得y=4，

∴C（0，4），

（2）

解：存在，

理由：∵B（4，0），C（0，4），

∴直线BC解析式为y=﹣x+4，

当直线BC向上平移b单位后和抛物线只有一个公共点时，△MBC面积最大，

∴ ，

∴x2﹣4x+b=0，

∴△=14﹣4b=0，

∴b=4，

∴ ，

∴M（2，6）

（3）

解：①如图，

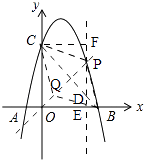
∵点P在抛物线上，

∴设P（m，﹣m2+3m+4），

当四边形PBQC是菱形时，点P在线段BC的垂直平分线上，

∵B（4，0），C（0，4）

∴线段BC的垂直平分线的解析式为y=x，

∴m=﹣m2+3m+4，

∴m=1± ，

∴P（1+ ，1+ ）或P（1﹣ ，1﹣ ），

②如图，

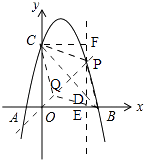
设点P（t，﹣t2+3t+4），

过点P作y轴的平行线l，过点C作l的垂线，

∵点D在直线BC上，

∴D（t，﹣t+4），

∵PD=﹣t2+3t+4﹣（﹣t+4）=﹣t2+4t，

BE+CF=4，

∴S四边形PBQC=2S△PDC=2（S△PCD+S△BD）=2（ PD×CF+ PD×BE）=4PD=﹣4t2+16t，

∵0＜t＜4，

∴当t=2时，S四边形PBQC最大=16

【解析】（1）用待定系数法求出抛物线解析式；（2）先判断出面积最大时，平移直线BC的直线和抛物线只有一个交点，从而求出点M坐标；（3）①先判断出四边形PBQC时菱形时，点P是线段BC的垂直平分线，利用该特殊性建立方程求解；②先求出四边形PBCQ的面积与t的函数关系式，从而确定出它的最大值．此题是二次函数综合题，主要考查了待定系数法，极值的确定，对称性，面积的确定，解本题的关键是确定出△MBC面积最大时，点P的坐标．