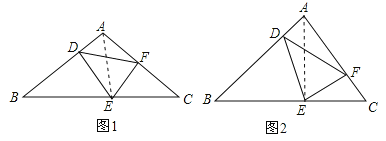
【题目】在△ABC中,点D,E,F分别在AB,BC,AC上,且∠ADF+∠DEC=180°,∠AFE=∠BDE.
(1)如图1,当DE=DF时,图1中是否存在与AB相等的线段?若存在,请找出,并加以证明;若不存在,说明理由;
(2)如图2,当DE=kDF(其中0<k<1)时,若∠A=90°,AF=m,求BD的长(用含k,m的式子表示).

参考答案:
【答案】(1)AB=BE;(2)BD=![]() .
.
【解析】
试题分析:(1)如图1,连结AE.由DE=DF,得到∠DEF=∠DFE,由∠ADF+∠DEC=180°,得到∠ADF=∠DEB.由∠AFE=∠BDE,得到∠AFE+∠ADE=180°,得到A、D、E、F四点共圆,由圆周角定理得出∠DAE=∠DFE=∠DEF,∠ADF=∠AEF.再由∠ADF=∠DEB=∠AEF,得出∠AEF+∠AED=∠DEB+∠AED,则∠AEB=∠DEF=∠BAE,由等角对等边得出AB=BE;
(2)如图2,连结AE.由A、D、E、F四点共圆,得到∠ADF=∠AEF,由∠DAF=90°,得到∠DEF=90°,再证明∠DEB=∠AEF.又∠AFE=∠BDE,得到△BDE∽△AFE,利用相似三角形对应边成比例得到![]() .在Rt△DEF中,利用勾股定理求出EF=
.在Rt△DEF中,利用勾股定理求出EF=![]() DF,然后将AF=m,DE=kDF代入,计算即可求解.
DF,然后将AF=m,DE=kDF代入,计算即可求解.
试题解析:(1)如图1,连结AE.∵DE=DF,∴∠DEF=∠DFE,∵∠ADF+∠DEC=180°,∴∠ADF=∠DEB,∵∠AFE=∠BDE,∴∠AFE+∠ADE=180°,∴A、D、E、F四点共圆,∴∠DAE=∠DFE=∠DEF,∠ADF=∠AEF,∵∠ADF=∠DEB=∠AEF,∴∠AEF+∠AED=∠DEB+∠AED,∴∠AEB=∠DEF=∠BAE,∴AB=BE;
(2)如图2,连结AE.∵∠AFE=∠BDE,∴∠AFE+∠ADE=180°,∴A、D、E、F四点共圆,∴∠ADF=∠AEF,∵∠DAF=90°,∴∠DEF=90°,∵∠ADF+∠DEC=180°,∴∠ADF=∠DEB,∵∠ADF=∠AEF,∴∠DEB=∠AEF,在△BDE与△AFE中,∵∠DEB=∠AEF,∠BDE=∠AFE,∴△BDE∽△AFE,∴![]() ,在直角△DEF中,∵∠DEF=90°,DE=kDF,∴EF=
,在直角△DEF中,∵∠DEF=90°,DE=kDF,∴EF=![]() =
=![]() DF,∴
DF,∴![]() =
=![]() ,∴BD=
,∴BD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,
①直径是弦;
②平分弦的直径必垂直于弦;
③相等的圆心角所对的弧相等;
④等弧所对的弦相等.
⑤经过半径的一端并垂直于半径的直线是圆的切线.正确的个数为( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E.

(1)若∠A=40°,求∠DCB的度数.
(2)若AE=4,△DCB的周长为13,求△ABC的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】把抛物线y=﹣2(x﹣2)2+3先向右平移1个单位长度,再向上平移2个单位长度后,所得函数的表达式为( )
A.y=﹣2(x﹣1)2+2B.y=﹣2(x+1)2+2
C.y=﹣2(x﹣3)2+5D.y=2(x﹣3)2+5
-
科目: 来源: 题型:
查看答案和解析>>【题目】情景:试根据图中信息,解答下列问题:
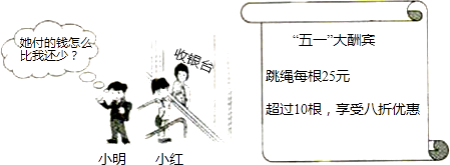
(1)购买6根跳绳需多少元,购买12根跳绳需多少元.
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b、c分别是△ABC的三边,其中a=1,c=4,且关于x的方程x2﹣4x+b=0有两个相等的实数根,试判断△ABC的形状.
-
科目: 来源: 题型:
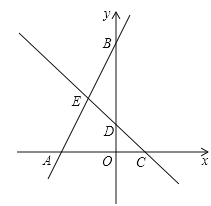
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+b与坐标轴交于C,D两点,直线AB与坐标轴交于A,B两点,线段OA,OC的长是方程
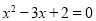 的两个根(OA>OC).
的两个根(OA>OC).(1)求点A,C的坐标;
(2)直线AB与直线CD交于点E,若点E是线段AB的中点,反比例函数
 (k≠0)的图象的一个分支经过点E,求k的值;
(k≠0)的图象的一个分支经过点E,求k的值;(3)在(2)的条件下,点M在直线CD上,坐标平面内是否存在点N,使以点B,E,M,N为顶点的四边形是菱形?若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.
相关试题

