【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;……依次类推,若第![]() 次操作余下的四边形是菱形,则称原平行四边形为
次操作余下的四边形是菱形,则称原平行四边形为![]() 阶准菱形,如图1,□
阶准菱形,如图1,□![]() 为1阶准菱形.
为1阶准菱形.
(1)猜想与计算
邻边长分别为3和5的平行四边形是 阶准菱形;已知□![]() 的邻边长分别为
的邻边长分别为![]() (
(![]() ),满足
),满足![]() ,
,![]() ,请写出□
,请写出□![]() 是 阶准菱形.
是 阶准菱形.
(2)操作与推理
小明为了剪去一个菱形,进行如下操作:如图2,把□![]() 沿
沿![]() 折叠(点
折叠(点![]() 在
在![]() 上),使点
上),使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,得到四边形
处,得到四边形![]() .请证明四边形
.请证明四边形![]() 是菱形.
是菱形.
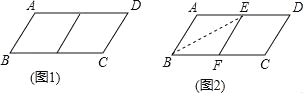
参考答案:
【答案】(1)3,12(2)证明见解析
【解析】
试题分析:(1)利用平行四边形准菱形的意义即可得出结论;
(2)先判断出∠AEB=∠ABE,进而判断出AE=BF,即可得出结论.
试题解析:(1)如图1,
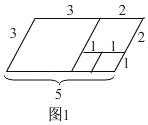
利用邻边长分别为3和5的平行四边形进行3次操作,所剩四边形是边长为1的菱形,
故邻边长分别为3和5的平行四边形是3阶准菱形:
如图2,
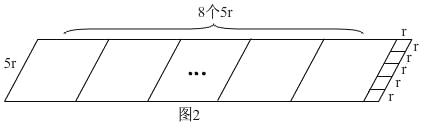
∵b=5r,
∴a=8b+r=40r+r=8×5r+r,
利用邻边长分别为41r和5r的平行四边形进行8+4=12次操作,所剩四边形是边长为1的菱形,
故邻边长分别为41r和5r的平行四边形是12阶准菱形:
故答案为:3,12
(2)由折叠知:∠ABE=∠FBE,AB=BF,
∵四边形ABCD是平行四边形,
∴AE∥BF,
∴∠AEB=∠FBE,
∴∠AEB=∠ABE,
∴AE=AB,
∴AE=BF,
∴四边形ABFE是平行四边形,
∴四边形ABFE是菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,Rt△ABC中,∠ACB=90°,AC=BC,∠ABC的角平分线交AC于E,AD⊥BE于D,求证:AD=
 BE.
BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多项式加上﹣2+x﹣x2得x2﹣1,则这个多项式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2+4x+4=0的根的情况是( )
A.有两个不相等的实数根B.有两个相等的实数根
C.有一个实数根D.没有实数根
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,抛物线
中,抛物线 过点
过点 ,,与
,,与 轴交于点
轴交于点 .
.(1)求抛物线
 的函数表达式;
的函数表达式;(2)若点
 在抛物线
在抛物线 的对称轴上,求
的对称轴上,求 的周长的最小值;
的周长的最小值;(3)在抛物线
 的对称轴上是否存在点
的对称轴上是否存在点 ,使
,使 是直角三角形?若存在,直接写出点
是直角三角形?若存在,直接写出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某玩具店用2000元购进一批玩具,面市后,供不应求,于是店主又购进同样的玩具,所购的数量是第一批数量的3倍,但进价贵了4元,结果购进第二批玩具共用了6300元,若两批玩具的售价都是120元,且两批玩具全部售完,求该玩具店销售这两批玩具共盈利多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|a+2|+(b﹣2)2=0,则ab=
相关试题

