【题目】如图,在四边形ABCD中,AD∥BC,AD=2,AB=2![]() ,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F
,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F
(1)求∠ABE的度数;
(2)用这个扇形AFED围成一个圆锥的侧面,所得圆锥的底面半径是多少?

参考答案:
【答案】(1)45°;(2)0.75.
【解析】连接AE,因为BC为圆A的切线,所以AE垂直于BC,所以三角形ABE为直角三角形,所以三角形ABE为等腰直角三角形,所以∠BAE为45°,因为∠AEB为直角,且AD平行于BC,所以∠DAE等于∠AEB等于90°,所以圆心角BAD等于45+90等于135°,弧FED的长等于![]() 乘以2π乘以2,等于1.5π,而扇形DAF为圆锥的侧面,所以弧长为圆锥的底面圆的周长,所以半径等于周长除以2π,所以半径等于0.75.
乘以2π乘以2,等于1.5π,而扇形DAF为圆锥的侧面,所以弧长为圆锥的底面圆的周长,所以半径等于周长除以2π,所以半径等于0.75.
解:(1)连接AE,如图1,

∵AD为半径的圆与BC相切于点E,
∴AE⊥BC,AE=AD=2.在Rt△AEB中,∵AB=2![]() , AE =2,由勾股定理得AE=BE,
, AE =2,由勾股定理得AE=BE,
∴∠ABE=45°.
(2)∵AD∥BC,
∴∠DAE=∠AEB=90°,
∴∠BAD45°+90°=135°,
∴扇形A-BFE的弧长=![]() =
=![]() .
.
设所得圆锥的底半径是r,
则2πr=![]() ,
,
∴r=0.75.
即:所得圆锥的底面半径是0.75.
“点睛”此题考查了切线的性质、直角三角形全等的判定与性质、等腰直角三角形的性质以及弧长公式.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 与
与 轴交于
轴交于 两点(
两点( 在左边),且过点
在左边),且过点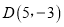 ,顶点为
,顶点为 ,直线
,直线 交
交 轴于点
轴于点 .
.(1)求
 的值;
的值;(2)以
 为直径画⊙P,问:点
为直径画⊙P,问:点 在⊙P上吗,为什么?
在⊙P上吗,为什么?(3)直线
 与⊙P存在怎样的位置关系?请说明理由.
与⊙P存在怎样的位置关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】八袋大米,以每袋25千克为标准,称重记录如下(超过标准的千克数记为正数,不足标准的千克数记为负数):+2,-0.5,+3,-1,+2,-1.5,+2.5,+4.这八袋大米总共有多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有以下3个说法:①垂线相等;②过一点有且只有一条直线与已知直线垂直;③过一点有且只有一条直线与已知直线平行.其中错误说法的个数是( )
A.0个 B.1个 C.2个 D.3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋子中装有大小、质地完全相同的4只小球,小球上分别标有1、2、3、4四个数字
(1)从袋中随机摸出一只小球,求小球上所标数字为奇数的概率;
(2)从袋中随机摸出一只小球,再从剩下的小球中随机摸出一只小球,求两次摸出的小球上所标数字之和为5的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中可能错误的是( )
A. 过一点有且只有一条直线与已知直线平行
B. 过一点有且只有一条直线与已知直线垂直
C. 两条直线相交,有且只有一个交点
D. 若两条直线相交成直角,则这两条直线互相垂直
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:(1)两点之间的所有连线中,线段最短;(2)相等的角是对顶角;(3)过一点有且仅有一条直线与已知直线平行;(4)长方体是四棱柱.其中正确的有______(填正确说法的序号).
相关试题

