【题目】如图,在![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 分别为
分别为![]() 边上的动点.
边上的动点.
(1)若点![]() 分别为
分别为![]() 的中点,求线段
的中点,求线段![]() 的长;
的长;
(2)若![]() ,
,
①求证: ![]() ∽
∽![]() ;
;
②试问![]() 与
与![]() 相似吗?并说明理由.
相似吗?并说明理由.

参考答案:
【答案】(1)EF=![]() ;(2)①证明见解析;②
;(2)①证明见解析;②![]() 与
与![]() 相似,理由见解析.
相似,理由见解析.
【解析】试题分析:(1)根据三角形的中位线的性质定理即可求解;
(2)由![]() ,
, ![]() 得∠A=∠B=45°,因为∠EOF=45°,所以∠BOE+∠AOF=135°,又∠BEO+∠BOE=135°,故∠BEO=∠AOF,从而可证ΔBOE∽ΔAFO;
得∠A=∠B=45°,因为∠EOF=45°,所以∠BOE+∠AOF=135°,又∠BEO+∠BOE=135°,故∠BEO=∠AOF,从而可证ΔBOE∽ΔAFO;
(3)由(2)得![]() ,因O为AB的中点得OA=OB,所以
,因O为AB的中点得OA=OB,所以![]() ,而∠B=∠EOF,故
,而∠B=∠EOF,故![]() ∽
∽![]() .
.
试题解析:(1)∵E、F分别为![]() 的中点
的中点
∴EF= ![]()
又∵![]() ,
, ![]()
∴AB=![]()
∴EF=![]()
(2) ①∵![]() ,
, ![]()
∴∠A=∠B=45°
又∵∠EOF=45°
∴∠BOE+∠AOF=135°
又∠BEO+∠BOE=135°
∴∠BEO=∠AOF
∴⊿BOE∽⊿AFO
②![]() 与
与![]() 相似,理由如下:
相似,理由如下:
由(2)得: ![]()
又∵O为AB的中点
∴OA=OB
∴![]()
又∵∠B=∠EOF
∴![]() ∽
∽![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC。其中一定能判断这个四边形是平行四边形的条件共有
A. 1组 B. 2组 C. 3组 D. 4组
-
科目: 来源: 题型:
查看答案和解析>>【题目】点(a,y1)(a+2,y2)都在反比例函数y=
 (k<0)的图象上,若y1>y2,则a的取值范围是_____.
(k<0)的图象上,若y1>y2,则a的取值范围是_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别是点D,E.
(1)求证:△BEC≌△CDA;
(2)当AD=3,BE=1时,求DE的长.
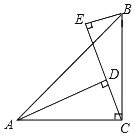
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数 yl= x ( x ≥0 ) ,
 ( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3
( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3  时, ③ 当 x =1时, BC = 8
时, ③ 当 x =1时, BC = 8④ 当 x 逐渐增大时, yl 随着 x 的增大而增大,y2随着 x 的增大而减小.其中正确结论的序号是_ .
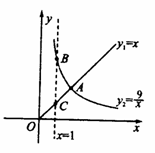
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
 的图象经过点A(x1,y1)和B(x2,y2)(x1<x2)
的图象经过点A(x1,y1)和B(x2,y2)(x1<x2)(1)若A(4,n)和B(n+
 ,3),求反比例函数的表达式;
,3),求反比例函数的表达式;(2)若m=1,
①当x2=1时,直接写出y1的取值范围;
②当x1<x2<0,p=
 ,q=
,q= ,试判断p,q的大小关系,并说明理由;
,试判断p,q的大小关系,并说明理由;(3)若过A、B两点的直线y=x+2与y轴交于点C,连接BO,记△COB的面积为S,当
 <S<1,求m的取值范围.
<S<1,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,8个完全相同的小矩形拼成了一个大矩形,AB是其中一个小矩形的对角线,请在大矩形中完成下列画图,要求:①仅用无刻度的直尺;②保留必要的画图痕迹.
(1)在图1中画出一个45°的角,使点A或者点B是这个角的顶点,且AB为这个角的一边.
(2)在图2中画出线段AB的垂直平分线.
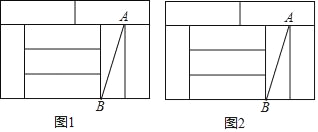
相关试题

