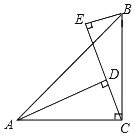
【题目】已知:如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别是点D,E.
(1)求证:△BEC≌△CDA;
(2)当AD=3,BE=1时,求DE的长.
参考答案:
【答案】(1)见解析;(2)2
【解析】
(1)根据垂直定义求出∠BEC=∠ACB=∠ADC,根据等式性质求出∠ACD=∠CBE,根据AAS证明△BCE≌△CAD;
(2)根据全等三角形的对应边相等得到AD=CE,BE=CD,利用DE=CE-CD,即可解答.
(1)证明:∵AD⊥CE,BE⊥CE,
∴∠ADC=∠E=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠∠CBE=90°,
∴∠ACD=∠CBE,
在△ADC和△CEB中,
 ,
,
∴△ADC≌△CEB(AAS),
(2)解:∵△ADC≌△CEB,
∴BE=CD=1,AD=EC=3,
∴DE=CE﹣CD=3﹣1=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点
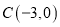 ,点
,点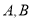 分别在
分别在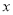 轴和
轴和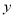 轴的正半轴上,且满足
轴的正半轴上,且满足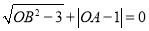 .
.(1)求点
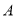 、点
、点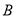 的坐标;
的坐标;(2)若点
 从点
从点 出发,以每秒1个单位长度的速度沿射线CB运动,连结AP,设
出发,以每秒1个单位长度的速度沿射线CB运动,连结AP,设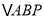 的面积为
的面积为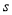 ,点
,点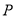 的运动时间为
的运动时间为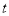 秒,求
秒,求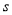 与
与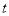 的函数关系式,并写出自变量
的函数关系式,并写出自变量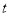 的取值范围;
的取值范围;(3)在(2)的条件下,是否存在点
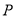 ,使得以点
,使得以点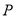 、
、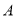 、
、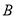 为顶点的三角形与
为顶点的三角形与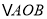 相似,若存在,请求出点
相似,若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.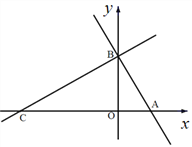
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC。其中一定能判断这个四边形是平行四边形的条件共有
A. 1组 B. 2组 C. 3组 D. 4组
-
科目: 来源: 题型:
查看答案和解析>>【题目】点(a,y1)(a+2,y2)都在反比例函数y=
 (k<0)的图象上,若y1>y2,则a的取值范围是_____.
(k<0)的图象上,若y1>y2,则a的取值范围是_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,  ,
,  ,点
,点 为
为 的中点,点
的中点,点 分别为
分别为 边上的动点.
边上的动点.(1)若点
 分别为
分别为 的中点,求线段
的中点,求线段 的长;
的长;(2)若
 ,
,①求证:
 ∽
∽ ;
;②试问
 与
与 相似吗?并说明理由.
相似吗?并说明理由.
-
科目: 来源: 题型:
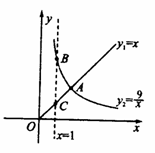
查看答案和解析>>【题目】函数 yl= x ( x ≥0 ) ,
 ( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3
( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3  时, ③ 当 x =1时, BC = 8
时, ③ 当 x =1时, BC = 8④ 当 x 逐渐增大时, yl 随着 x 的增大而增大,y2随着 x 的增大而减小.其中正确结论的序号是_ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
 的图象经过点A(x1,y1)和B(x2,y2)(x1<x2)
的图象经过点A(x1,y1)和B(x2,y2)(x1<x2)(1)若A(4,n)和B(n+
 ,3),求反比例函数的表达式;
,3),求反比例函数的表达式;(2)若m=1,
①当x2=1时,直接写出y1的取值范围;
②当x1<x2<0,p=
 ,q=
,q= ,试判断p,q的大小关系,并说明理由;
,试判断p,q的大小关系,并说明理由;(3)若过A、B两点的直线y=x+2与y轴交于点C,连接BO,记△COB的面积为S,当
 <S<1,求m的取值范围.
<S<1,求m的取值范围.
相关试题

