【题目】已知反比例函数y=![]() 的图象经过点A(x1,y1)和B(x2,y2)(x1<x2)
的图象经过点A(x1,y1)和B(x2,y2)(x1<x2)
(1)若A(4,n)和B(n+![]() ,3),求反比例函数的表达式;
,3),求反比例函数的表达式;
(2)若m=1,
①当x2=1时,直接写出y1的取值范围;
②当x1<x2<0,p=![]() ,q=
,q=![]() ,试判断p,q的大小关系,并说明理由;
,试判断p,q的大小关系,并说明理由;
(3)若过A、B两点的直线y=x+2与y轴交于点C,连接BO,记△COB的面积为S,当![]() <S<1,求m的取值范围.
<S<1,求m的取值范围.
参考答案:
【答案】(1)y=![]() ;(2)①当0<x1<1时,y1>1,当x1<0时,y1<0;②p<q,见解析;(3)
;(2)①当0<x1<1时,y1>1,当x1<0时,y1<0;②p<q,见解析;(3)![]() <m<3或-1<m<-
<m<3或-1<m<-![]()
【解析】
(1)将点A,B的坐标代入反比例函数解析式中,联立方程组即可得出结论;
(2)先得出反比例函数解析式,
①先得出x1=![]() ,再分两种情况讨论即可得出结论;
,再分两种情况讨论即可得出结论;
②先表示出y1=![]() ,y2=
,y2=![]() ,进而得出p=
,进而得出p=![]() ,最后用作差法,即可得出结论;
,最后用作差法,即可得出结论;
(3)先用m表示出x2=-1+![]() ,再求出点C坐标,进而用x2表示出S,再分两种情况用
,再求出点C坐标,进而用x2表示出S,再分两种情况用![]() <S<1确定出x2的范围,即可得出-1+
<S<1确定出x2的范围,即可得出-1+![]() 的范围,即可得出m的范围.
的范围,即可得出m的范围.
解:(1)∵A(4,n)和B(n+![]() ,3)在反比例函数y=
,3)在反比例函数y=![]() 的图象上,
的图象上,
∴4n=3(n+![]() )=m,
)=m,
∴n=1,m=4,
∴反比例函数的表达式为y=![]() ;
;
(2)∵m=1,
∴反比例函数的表达式为y=![]() ,
,
①如图1,∵B(x2,y2)在反比例函数y=![]() 的图象上,
的图象上,
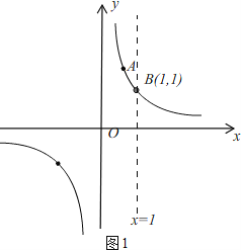
∴y2=1,
∴B(1,1),
∵A(x1,y1)在反比例函数y=![]() 的图象上,
的图象上,
∴y1=![]() ,
,
∴x1=![]() ,
,
∵x1<x2,x2=1,
∴x1<1,
当0<x1<1时,y1>1,
当x1<0时,y1<0;
②p<q,理由:∵反比例函数y=![]() 的图象经过点A(x1,y1)和B(x2,y2),
的图象经过点A(x1,y1)和B(x2,y2),
∴y1=![]() ,y2=
,y2=![]() ,
,
∴p=![]() =
=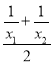 =
=![]() ,
,
∵q=![]() ,
,
∴p-q=![]() -
-![]() =
=![]() =
=![]() ,
,
∵x1<x2<0,
∴(x1+x2)2>0,x1x2>0,x1+x2<0,
∴![]() <0,
<0,
∴p-q<0,
∴p<q;
(3)∵点B(x2,y2)在直线AB:y=x+2上,也在在反比例函数y=![]() 的图象上,
的图象上,
∴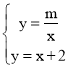 ,解得,x=-1
,解得,x=-1![]() ,
,
∵x1<x2,
∴x2=-1+![]()
∵直线AB:y=x+2与y轴相交于点C,
∴C(0,2),
当m>0时,如图2,

∵A(x1,y1)和B(x2,y2)(x1<x2),
∴点B的横坐标大于0,
即:x2>0
∴S=![]() OCx2=
OCx2=![]() ×2×x2=x2,
×2×x2=x2,
∵![]() <S<1,
<S<1,
∴![]() <x2<1,
<x2<1,
∴![]() <-1+
<-1+![]() <1,
<1,
∴![]() <m<3;
<m<3;
当m<0时,如图3,∵A(x1,y1)和B(x2,y2)(x1<x2),
∴点B的横坐标小于0,

即:x2<0
∴S=![]() OC|x2|=-
OC|x2|=-![]() ×2×x2=-x2,
×2×x2=-x2,
∵![]() <S<1,
<S<1,
∴![]() <-x2<1,
<-x2<1,
∴-1<x2<-![]() ,
,
∴-1<-1+![]() <-
<-![]() ,
,
∴-1<m<-![]() ,
,
即:当![]() <S<1时,m的取值范围为
<S<1时,m的取值范围为![]() <m<3或-1<m<-
<m<3或-1<m<-![]() .
.
-
科目: 来源: 题型:
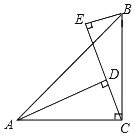
查看答案和解析>>【题目】已知:如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别是点D,E.
(1)求证:△BEC≌△CDA;
(2)当AD=3,BE=1时,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,  ,
,  ,点
,点 为
为 的中点,点
的中点,点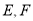 分别为
分别为 边上的动点.
边上的动点.(1)若点
 分别为
分别为 的中点,求线段
的中点,求线段 的长;
的长;(2)若
 ,
,①求证:
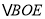 ∽
∽ ;
;②试问
 与
与 相似吗?并说明理由.
相似吗?并说明理由.
-
科目: 来源: 题型:
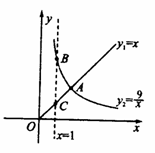
查看答案和解析>>【题目】函数 yl= x ( x ≥0 ) ,
 ( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3
( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3  时, ③ 当 x =1时, BC = 8
时, ③ 当 x =1时, BC = 8④ 当 x 逐渐增大时, yl 随着 x 的增大而增大,y2随着 x 的增大而减小.其中正确结论的序号是_ .
-
科目: 来源: 题型:
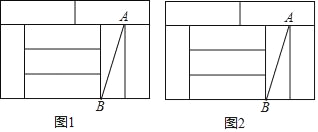
查看答案和解析>>【题目】如图,8个完全相同的小矩形拼成了一个大矩形,AB是其中一个小矩形的对角线,请在大矩形中完成下列画图,要求:①仅用无刻度的直尺;②保留必要的画图痕迹.
(1)在图1中画出一个45°的角,使点A或者点B是这个角的顶点,且AB为这个角的一边.
(2)在图2中画出线段AB的垂直平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】密码锁有三个转轮,每个转轮上有十个数字:0,1,2,…9.小黄同学是9月份中旬出生,用生日“月份+日期”设置密码:9××
小张同学要破解其密码:
(1)第一个转轮设置的数字是9,第二个转轮设置的数字可能是 .
(2)请你帮小张同学列举出所有可能的密码,并求密码数能被3整除的概率;
(3)小张同学是6月份出生,根据(1)(2)的规律,请你推算用小张生日设置的密码的所有可能个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本
(1)求每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
相关试题

