【题目】如图,甲船逆水,静水速度为28海里/时;乙船顺水,静水速度为12海里/时,两船相距60海里.已知水流速度为3海里/时,两船同时相向而行.
(1)两船同时航行1小时,求此时两船之间的距离;
(2)再(1)的情况下,两船再继续航行1小时,求此时两船之间的距离;
(3)求两船从开始航行到两船相距12海里,需要多长时间?

参考答案:
【答案】(1) 20海里;(2) 20海里;(3) 1.2小时或1.8小时.
【解析】
(1)根据1h后甲、乙间的距离=两船相距-(甲船行驶的路程+乙船行驶的路程)即可得;
(2)根据2h后甲、乙间的距离=甲船行驶的路程-乙船行驶的路程即可得;
(3)可分相遇前与相遇后两种情况讨论即可解答.
解:根据题意可知甲船的行驶速度为28-3=25海里/时,乙船的行驶速度为12+3=15海里/时
(1)1h后甲、乙间的距离=60-25×1-15×1=20海里;
(2)2h后甲、乙间的距离=25×2-15×2=20海里;
(3)相遇前,设两船从开始航行到两船相距12海里,需要t小时
则12=60-(25+15)t,求得t=1.2小时
相遇后,设两船从开始航行到两船相距12海里,需要t1小时
则12+60=(25+15)t1,求得t1=1.8小时
故两船从开始航行到两船相距12海里,1.2小时或1.8小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】按如图所示的程序计算.若开始输入的
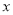 的值为18,我们发现第1次得到的结果为9,第2次得到的结果为14,第3次得到的结果为7.……,请你探索第2019次得到的结果为_________.
的值为18,我们发现第1次得到的结果为9,第2次得到的结果为14,第3次得到的结果为7.……,请你探索第2019次得到的结果为_________.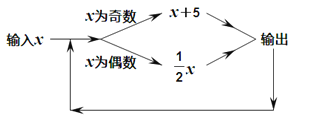
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
星期
一
二
三
四
五
六
日
增减(辆)
-1
+3
-2
-4
+7
-5
-10
(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总的生产量是多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了弘扬中华传统文化,了解学生整体阅读能力,组织全校的1000名学生进行一次阅读理解大赛.从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制了频数分布表和频数分布直方图:
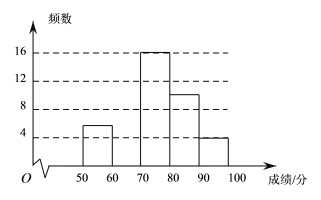
分组/分
频数
频率
50≤x<60
6
0.12
60≤x<70

0.28
70≤x<80
16
0.32
80≤x<90
10
0.20
90≤x≤100
4
0.08
(1)频数分布表中的
 ;
;(2)将上面的频数分布直方图补充完整;
(3)如果成绩达到90及90分以上者为优秀,可推荐参加决赛,估计该校进入决赛的学生大约有 人.
-
科目: 来源: 题型:
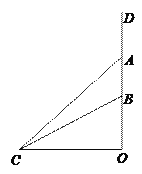
查看答案和解析>>【题目】如图,水渠边有一棵大木瓜树,树干
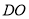 (不计粗细)上有两个木瓜
(不计粗细)上有两个木瓜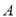 ,
,  (不计大小),树干垂直于地面,量得
(不计大小),树干垂直于地面,量得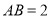 m,在水渠的对面与
m,在水渠的对面与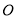 处于同一水平面的
处于同一水平面的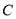 处测得木瓜
处测得木瓜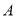 的仰角为45°、木瓜
的仰角为45°、木瓜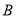 的仰角为30°.求
的仰角为30°.求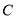 处到树干
处到树干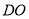 的距离
的距离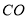 (结果精确到1m)(参考数据:
(结果精确到1m)(参考数据: 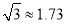 ,
, 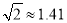 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一位运动员推铅球,铅球运行时离地面的高度
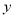 (米)是关于运行时间
(米)是关于运行时间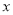 (秒)的二次函数.已知铅球刚出手时离地面的高度为
(秒)的二次函数.已知铅球刚出手时离地面的高度为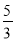 米;铅球出手后,经过4秒到达离地面3米的高度,经过10秒落到地面.如图建立平面直角坐标系.
米;铅球出手后,经过4秒到达离地面3米的高度,经过10秒落到地面.如图建立平面直角坐标系.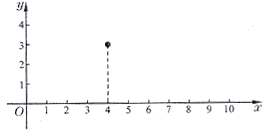
(Ⅰ)为了求这个二次函数的解析式,需要该二次函数图象上三个点的坐标.根据题意可知,该二次函数图象上三个点的坐标分别是____________________________;
(Ⅱ)求这个二次函数的解析式和自变量
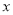 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
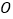 为坐标原点,点
为坐标原点,点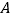 (0,1),点
(0,1),点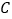 (1,0),正方形
(1,0),正方形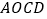 的两条对角线的交点为
的两条对角线的交点为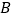 ,延长
,延长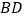 至点
至点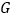 ,使
,使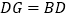 .延长
.延长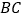 至点
至点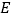 ,使
,使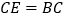 ,以
,以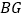 ,
,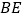 为邻边做正方形
为邻边做正方形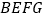 .
.(Ⅰ)如图①,求
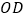 的长及
的长及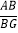 的值;
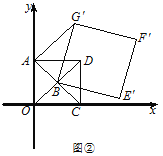
的值;(Ⅱ)如图②,正方形
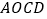 固定,将正方形
固定,将正方形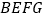 绕点
绕点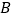 逆时针旋转,得正方形
逆时针旋转,得正方形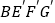 ,记旋转角为
,记旋转角为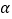 (0°<
(0°<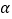 <360°),连接
<360°),连接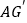 .
.①旋转过程中,当
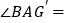 90°时,求
90°时,求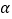 的大小;
的大小;②在旋转过程中,求
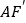 的长取最大值时,点
的长取最大值时,点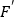 的坐标及此时
的坐标及此时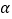 的大小(直接写出结果即可).
的大小(直接写出结果即可).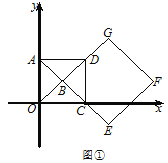
相关试题

