【题目】在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() (0,1),点
(0,1),点![]() (1,0),正方形
(1,0),正方形![]() 的两条对角线的交点为
的两条对角线的交点为![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() .延长
.延长![]() 至点
至点![]() ,使
,使![]() ,以
,以![]() ,
,![]() 为邻边做正方形
为邻边做正方形![]() .
.
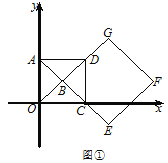
(Ⅰ)如图①,求![]() 的长及
的长及![]() 的值;
的值;
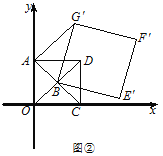
(Ⅱ)如图②,正方形![]() 固定,将正方形
固定,将正方形![]() 绕点
绕点![]() 逆时针旋转,得正方形
逆时针旋转,得正方形![]() ,记旋转角为
,记旋转角为![]() (0°<
(0°<![]() <360°),连接
<360°),连接![]() .
.
①旋转过程中,当![]() 90°时,求
90°时,求![]() 的大小;
的大小;
②在旋转过程中,求![]() 的长取最大值时,点
的长取最大值时,点![]() 的坐标及此时
的坐标及此时![]() 的大小(直接写出结果即可).
的大小(直接写出结果即可).
参考答案:
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)①
;(Ⅱ)①![]() 30°,
30°,![]() 150°,②
150°,②![]() (
(![]() ,
,![]() ),
),![]() 315°.
315°.
【解析】试题分析:(Ⅰ)根据正方形的性质以及勾股定理即可解决问题;
(Ⅱ)①因为∠BAG′=90°,BG′=2AB,可知sin∠AG′B=![]() =
=![]() ,推出∠AG′B=30°,推出旋转角α=30°,据对称性可知,当∠ABG″=60°时,∠BAG″=90°,也满足条件,此时旋转角α=150°;
,推出∠AG′B=30°,推出旋转角α=30°,据对称性可知,当∠ABG″=60°时,∠BAG″=90°,也满足条件,此时旋转角α=150°;
②当α=315°时,A、B、F′在一条直线上时,AF′的长最大.
试题解析:解:(Ⅰ)如图1中,∵A(0,1),∴OA=1.∵四边形OADC是正方形,∴∠OAD=90°,AD=OA=1,∴OD=AC=![]() =
=![]() ,∴AB=BC=BD=BO=
,∴AB=BC=BD=BO=![]() .∵BD=DG,∴BG=
.∵BD=DG,∴BG=![]() ,∴
,∴![]() =
=![]() =
=![]() .
.
(Ⅱ)①如图2中,∵∠BAG′=90°,BG′=2AB,∴sin∠AG′B=![]() =
=![]() ,∴∠AG′B=30°,∴∠ABG′=60°,∴∠DBG′=30°,∴旋转角α=30°,根据对称性可知,当∠ABG″=60°时,∠BAG″=90°,也满足条件,此时旋转角α=150°.
,∴∠AG′B=30°,∴∠ABG′=60°,∴∠DBG′=30°,∴旋转角α=30°,根据对称性可知,当∠ABG″=60°时,∠BAG″=90°,也满足条件,此时旋转角α=150°.
综上所述:旋转角α=30°或150°时,∠BAG′=90°.
②如图3中,连接OF.∵四边形BE′F′G′是正方形的边长为![]() ,∴BF′=2,∴当α=315°时,A、B、F′在一条直线上时,AF′的长最大,最大值为
,∴BF′=2,∴当α=315°时,A、B、F′在一条直线上时,AF′的长最大,最大值为![]() +2,此时α=315°,F′(
+2,此时α=315°,F′(![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲船逆水,静水速度为28海里/时;乙船顺水,静水速度为12海里/时,两船相距60海里.已知水流速度为3海里/时,两船同时相向而行.
(1)两船同时航行1小时,求此时两船之间的距离;
(2)再(1)的情况下,两船再继续航行1小时,求此时两船之间的距离;
(3)求两船从开始航行到两船相距12海里,需要多长时间?

-
科目: 来源: 题型:
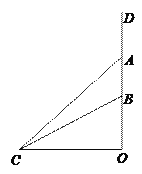
查看答案和解析>>【题目】如图,水渠边有一棵大木瓜树,树干
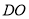 (不计粗细)上有两个木瓜
(不计粗细)上有两个木瓜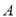 ,
,  (不计大小),树干垂直于地面,量得
(不计大小),树干垂直于地面,量得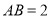 m,在水渠的对面与
m,在水渠的对面与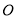 处于同一水平面的
处于同一水平面的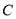 处测得木瓜
处测得木瓜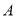 的仰角为45°、木瓜
的仰角为45°、木瓜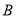 的仰角为30°.求
的仰角为30°.求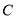 处到树干
处到树干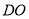 的距离
的距离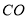 (结果精确到1m)(参考数据:
(结果精确到1m)(参考数据: 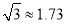 ,
, 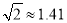 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一位运动员推铅球,铅球运行时离地面的高度
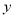 (米)是关于运行时间
(米)是关于运行时间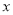 (秒)的二次函数.已知铅球刚出手时离地面的高度为
(秒)的二次函数.已知铅球刚出手时离地面的高度为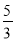 米;铅球出手后,经过4秒到达离地面3米的高度,经过10秒落到地面.如图建立平面直角坐标系.
米;铅球出手后,经过4秒到达离地面3米的高度,经过10秒落到地面.如图建立平面直角坐标系.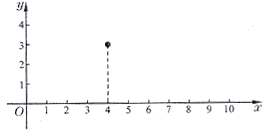
(Ⅰ)为了求这个二次函数的解析式,需要该二次函数图象上三个点的坐标.根据题意可知,该二次函数图象上三个点的坐标分别是____________________________;
(Ⅱ)求这个二次函数的解析式和自变量
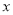 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
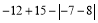
(2)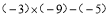
(3)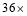 (
(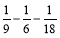 )
)
(4)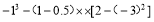
(5)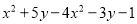
(6)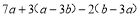
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,对角线BD平分∠ABC,过点A作AE∥BD,交CD的延长线于点E,过点E作EF⊥BC,交BC的延长线于点F.
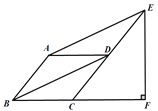
(1)求证:四边形ABCD是菱形;(2)若∠ABC=45°,BC=1,求EF的长.
-
科目: 来源: 题型:
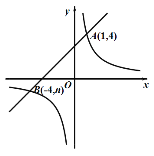
查看答案和解析>>【题目】如图,已知反比例函数
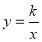 的图像与一次函数
的图像与一次函数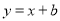 的图像交于点
的图像交于点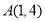 ,点
,点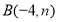 .
.
(1)求k和b的值;
(2)连接OA、OB,求
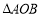 的面积;
的面积;(3)利用图像,直接写出
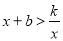 时x的取值范围.
时x的取值范围.
相关试题

