【题目】已知二次函数的图象经过点(2,3),顶点坐标(1,4)
(1)求该二次函数的解析式;
(2)图象与x轴的交点为A、B,与y轴的交点为C,求△ABC的面积.
参考答案:
【答案】(1)y=-(x-1)2+4;(2)S△ABC=6.
【解析】
(1)设出二次函数的顶点式y=a(x-1)2+4,将点(2,3)代入解析式,求出a的值即可得到函数解析式;
(2)令y=0,据此即可求出函数与x轴交点的横坐标,从而得到图象与x轴交点A、B两点的坐标;由于知道C点坐标,根据A、B的坐标,求出AB的长,利用三角形的面积公式求出三角形的面积.
(1)设所求的二次函数的解析式为y= a(x-1)2+4,
把x=2,y=3代入上式,得:
3=a(2-1)2+4,
解得:a=1,
∴所求的二次函数解析式为y=(x-1)2+4,
即y=x2+2x+3.
(2)当y=0时,0= x2+2x+3,
解得:![]() =1,
=1,![]() =3,
=3,
∴图象与x轴交点A. B两点的坐标分别为(1,0),(3,0),
由题意得:C点坐标为(0,3),AB=4,
∴S△ABC= ![]() ×4×3=6.
×4×3=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式及其展开式
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
…
根据下图,猜想:
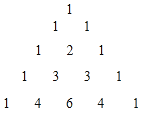
(a+b)5=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,∠B=90°,点D为直线BC上一个动点(不与B,C重合),连结AD.将线段AD绕点D按顺吋针方向旋转90°得到线段DE,连结EC.
(1)如图1,点D在线段BC上,依题意画图得到图2.
①求证:∠BAD=∠EDC;
②方方同学通过观察、测量得出结论:在点D运动的过程中,总有∠DCE=135°.方方的主要思路有以下几个:
思路一:在AB上取一点F使得BF=BD,要证∠DCE=135°,只需证△ADF≌△DEC.
思路二:以点D为圆心,DC为半径画弧交AC于点F,要证∠DCE=135°,只需证△AFD≌△ECD.
思路三:过点E作BC所在直线的垂线段EF,要证∠DCE=135°,只需证EF=CF.
……
请你参考井选择其中一个思路,证明∠DCE=135°;
(2)如果点D在线段CB的延长线上运动,利用图3画图分析,∠DCE的度数还是确定的值吗?如果是,请写出∠DCE的度数并说明理由;如果不是,也请说明你的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列文字与例题,并解答。
将一个多项式分组进行因式分解后,可用提公因式法或公式法继续分解的方法称作分组分解法。例如:以下式子的分解因式的方法叉称为分组分解法。
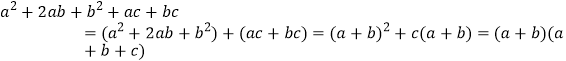 (1)试用“分组分解法”分解因式:
(1)试用“分组分解法”分解因式:
(2)已知四个实数a,b,c,d满足
 。并且
。并且 ,
, ,
, ,
, 同时成立。
同时成立。①当k=1时,求a+c的值;
②当k≠0时,用含a的代数式分别表示b、c、d。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,∠CAB=30°
求:(1)求∠ADC的度数;
(2)如果OE⊥AC,垂足为E,求OE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有颜色不同的红、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
摸球的次数n
100
150
200
500
800
1000
摸到白球的次数
38
51
76
195
324
401
摸到白球的频率
0.38
0.34
0.38
0.39
0.405
0.401
(1)请估计:当n很大时,摸到白球的频率将会接近_______;(精确到0.1)
(2)试估算口袋中白球有多少只?
(3)请画树状图或列表计算:从中先摸出一球,不放回,再摸出一球;摸到两只白球的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是⊙O的直径,半径OC垂直AB,D为弧AC上任意一点,E为弦BD上一点,且BE=AD
(1)试判断△CDE的形状,并加以证明.
(2)若∠ABD=15°,AO=4,求DE的长.

相关试题

