Question

【题目】已知AB是⊙O的直径，半径OC垂直AB，D为弧AC上任意一点，E为弦BD上一点，且BE=AD

（1）试判断△CDE的形状，并加以证明．

（2）若∠ABD=15°，AO=4，求DE的长．

Answer 1

【答案】（1）△CDE为等腰直角三角形，证明详见解析；（2）.

【解析】

（1）由条件可证明△ADC≌△BEC，则可得到CD=CE，结合AB为直径可证明∠DCE=90°，可判断△CDE为等腰直角三角形；
（2）由条件可证明△COD为等边三角形，则可求得CD=4，利用勾股定理可求得DE的长．

(1)△CDE为等腰直角三角形，

证明如下：

如图1，连接AC、BC，

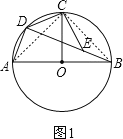
则∠DAC=∠DBC，

∵AB为直径，CO⊥AB，

∴△ABC为等腰直角三角形，

∴AC=BC，

在△ADC和△BEC中

∴△ADC≌△BEC(SAS)，

∴CD=CE，∠DCA=∠BCE，

∵∠ACB=90°，

∴∠ACE+∠BCE=90°，

∴∠DCA+∠ACE=90°,即∠DCE=90°，

∴△CDE为等腰直角三角形；

(2)如图2，连接OD，

则∠AOD=2∠ABD=2×15°=30°，

∵∠AOC=90°，

∴∠DOC=60°，且OD=OC=OA=4，

∴△OCD为等边三角形，

∴CD=CE=OA=4，

在Rt△CDE中,由勾股定理可得.