【题目】(1)如图甲,AB∥CD,试问∠2与∠1+∠3的关系是什么,为什么?
(2)如图乙,AB∥CD,试问∠2+∠4与∠1+∠3+∠5一样大吗?为什么?
(3)如图丙,AB∥CD,试问∠2+∠4+∠6与∠1+∠3+∠5+∠7哪个大?为什么?
你能将它们推广到一般情况吗?请写出你的结论.
参考答案:
【答案】解:(1)∠2=∠1+∠3.
过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=∠1,∠CEF=∠3,
∴∠2=∠BEF+∠CEF=∠1+∠3;
(2)∠2+∠4=∠1+∠3+∠5.
分别过点E,G,M,作EF∥AB,GH∥AB,MN∥AB,
∵AB∥CD,
∴AB∥CD∥EF∥GH∥MN,
∴∠1=∠BEF,∠FEG=∠EGH,∠HGM=∠GMN,∠CMN=∠5,
∴∠2+∠4=∠BEF+∠FEG+∠GMN+∠CMN=∠1+∠EGH+∠MGH+∠5=∠1+∠3+∠5;
(3)∠2+∠4+∠6=∠1+∠3+∠5+∠7.
分别过点E,G,M,K,P,作EF∥AB,GH∥AB,MN∥AB,KL∥AB,PQ∥AB,
∵AB∥CD,
∴AB∥CD∥EF∥GH∥MN∥KL∥PQ,
∴∠1=∠BEF,∠FEG=∠EGH,∠HGM=∠GMN,∠KMN=∠LKM,∠LKP=∠KPQ,∠QPC=∠7,
∴∠2+∠4+∠6=∠1+∠3+∠5+∠7.
归纳:开口朝左的所有角度之和与开口朝右的所有角度之和相等.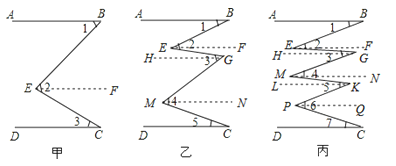
【解析】(1)首先过点E作EF∥AB,由AB∥CD,可得AB∥CD∥EF,根据平行线的性质,易得∠2=∠BEF+∠CEF=∠1+∠3;
(2)首先分别过点E,G,M,作EF∥AB,GH∥AB,MN∥AB,由AB∥CD,可得AB∥CD∥EF∥GH∥MN,由平行线的性质,可得∠2+∠4=∠1+∠3+∠5.
(3)首先分别过点E,G,M,K,P,作EF∥AB,GH∥AB,MN∥AB,KL∥AB,PQ∥AB,由AB∥CD,可得AB∥CD∥EF∥GH∥MN∥KL∥PQ,然后利用平行线的性质,即可证得∠2+∠4+∠6=∠1+∠3+∠5+∠7.
【考点精析】本题主要考查了平行线的性质的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】温州一位老人制作的仿真郑和宝船尺寸如图,已知在某一直角坐标系中,点A坐标为(9,0).
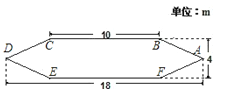
(1)请你直接在图中画出该坐标系;
(2)写出其余5点的坐标;
(3)仿真郑和宝船图中互相平行的线段有哪些?分别写出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解正确的是( )
A. m3+m2+m=m(m2+m) B. x3﹣x=x(x2﹣1)
C. (a+b)(a﹣b)=a2﹣b2 D. ﹣4a2+9b2=(﹣2a+3b)(2a+3b)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明想测量学校教学楼的高度,教学楼AB的后面有一建筑物CD,他测得当光线与地面成22°的夹角时,教学楼在建筑物的墙上留下高2m高的影子CE;而当光线与地面成45°的夹角时,教学楼顶A在地面上的影子F与墙角C有13m的距离(点B,F,C在同一条直线上)
(1)请你帮小明计算一下学校教学楼的高度;
(2)为了迎接上级领导检查,学校准备在AE之间挂一些彩旗,请计算AE之间的长.(结果精确到1m,参考数据:sin22°≈0.375,cos22°≈0.9375,tan22°≈0.4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】a与5的和的3倍用代数式表示是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB和CD相交于点O,∠C=∠1,∠D=∠2,求证:∠A=∠B.
证明:∵∠C=∠1,∠D=∠2(已知)
又∵∠1=∠2( )
∴ ( )
∴AC∥BD( )
∴ (两直线平行,内错角相等)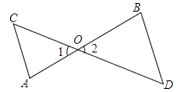
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们在学习“实数”时,画了这样一个图,即“以数轴上的单位长为‘1’的线段作一个正方形,然后以原点O为圆心,正方形的对角线长为半径画弧交x轴于点A”,请根据图形回答下列问题:
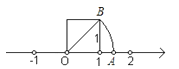
(1)线段OA的长度是多少?(要求写出求解过程)
(2)这个图形的目的是为了说明什么?
(3)这种研究和解决问题的方式,体现了 的数学思想方法.
(将下列符合的选项序号填在横线上)
A、数形结合;B、代入;C、换元;D、归纳.
相关试题

