【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据题中所给信息解答以下问题:
(1)甲、乙两地之间的距离为____km;图中点C的实际意义为:______;慢车的速度为_______,快车的速度为______;
(2)求线段BC所表示的y与x之间的函数关系式,以及自变量x的取值范围;
(3)若在第一列快车与慢车相遇时,第二列快车从乙地出发驶往甲地,速度与第一列快车相同.请直接写出第二列快车出发多长时间,与慢车相距200km.
(4)若第三列快车也从乙地出发驶往甲地,速度与第一列快车相同.如果第三列快车不能比慢车晚到,求第三列快车比慢车最多晚出发多少小时?

参考答案:
【答案】(1)960;当慢车行驶6 h时,快车到达乙地;80km/h;160km/h;(2)y=240x﹣960(4≤x≤6);(3)第二列快车出发1.5h,与慢车相距200km;(4)第三列快车比慢车最多晚出发6小时.
【解析】
(1)根据图象即可看出甲乙两地之间的距离,根据图可知:慢车行驶的时间是12h、快车行驶的时间是6h,根据速度公式求出速度即可;
(2)设线段BC所表示的y与x之间的函数关系式为y=kx+b,根据所显示的数据求出B和C的坐标,代入求出即可;
(3)分为两种情况:①设第二列快车出发ah,与慢车相距200km,根据题意得出方程4×80+80a-200=160a,求出即可;
②第二列开车追上慢车以后再超过慢车200km,设第二列快车出发ah,与慢车相距200km,则160a-80a=4×80+200,求出即可;
(4)设第三列快车在慢车出发t h后出发.得出不等式t+![]() ≤
≤![]() ,求出不等式的解集即可.
,求出不等式的解集即可.
解:(1)由图象可知,甲、乙两地之间的距离是960km;
图中点C的实际意义是:当慢车行驶6 h时,快车到达乙地;
慢车的速度是:960km÷12h=80km/h;
快车的速度是:960km÷6h=160km/h;
故答案为:960;当慢车行驶6 h时,快车到达乙地;80km/h;160km/h;
(2)根据题意,两车行驶960km相遇,所用时间![]() =4(h),
=4(h),
所以点B的坐标为(4,0),两小时两车相距2×(160+80)=480(km),
所以点C的坐标为(6,480).
设线段BC所表示的y与x之间的函数关系式为y=kx+b,把(4,0),(6,480)代入得![]() ,
,
解得![]() .
.
所以,线段BC所表示的y与x之间的函数关系式为y=240x﹣960,自变量x的取值范围是4≤x≤6.
(3)分为两种情况:①设第二列快车出发ah,与慢车相距200km,
则4×80+80a﹣200=160a,
解得:a=1.5,
即第二列快车出发1.5h,与慢车相距200km;
②第二列开车追上慢车以后再超过慢车200km.
设第二列快车出发ah,与慢车相距200km,
则160a﹣80a=4×80+200,得a=6.5>6,(因为快车到达甲地仅需6小时,所以a=6.5舍去)
综合这两种情况得出:第二列快车出发1.5h,与慢车相距200km.
(4)设第三列快车在慢车出发t h后出发.
则t+![]() ≤
≤![]() ,
,
解得:t≤6.
故第三列快车比慢车最多晚出发6小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 y=x2+bx+c与x
y=x2+bx+c与x 轴交于A(-2,0),B(6,0)两点.
轴交于A(-2,0),B(6,0)两点.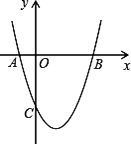
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)点P为y轴右侧抛物线上一个动点,若S△PAB=32,求出此时P点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AC,点D为AC的中点,B是直线AC上的一点,且 BC=
 AB,BD=1cm,则线段AC的长为( )
AB,BD=1cm,则线段AC的长为( )A.
 B.
B.  C.
C.  或
或 D.
D.  或
或
-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数 y=ax2+bx+c(a<0) 的图象经过点(2,0),且其对称轴为直线 x=1 ,则使函数值 y>0 成立的 x 的取值范围是( )
A. x<4 或 x>2
x<4 或 x>2
B. 4 ≤ x ≤ 2
4 ≤ x ≤ 2
C. x ≤ 4 或 x ≥ 2
x ≤ 4 或 x ≥ 2
D. 4<x<2
4<x<2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,菱形ABCD的边长为a,点O是对角线AC上的一点,且OA=a,OB=OC=OD=1,则a等于( )

A.
B.
C.1
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 ,
, .
.(1)求B;(用含a、b的代数式表示)
(2)比较A与B的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰直角△ABC中,AC=BC>3,点M在AC上,点N在CB的延长线上,MN交AB于点O,且AM=BN=3,则S△AMO与S△BNO的差是( )

A.9
B.4.5
C.0
D.无法确定
相关试题

