【题目】已知数轴上有A. B.C三点,分别表示有理数26,10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设点P移动时间为t秒。

(1)PA= ,PC= (用含t的代数式表示)
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,当点P运动到点C时,P、Q两点运动停止,
①当P、Q两点运动停止时,求点P和点Q的距离;
②求当t为何值时P、Q两点恰好在途中相遇.
参考答案:
【答案】(1)t;36-t;(2)①24;②30.
【解析】
(1)利用数轴上两点的距离公式求出AC的长度,根据路程=速度×时间,用t表示出AP,
再利用PC=AC-AP即可;
(2)①先利用数轴上两点的距离公式求出BC的长度,再利用时间=路程÷速度算出P从B运动到C的时间,算出Q的运动路程,最后减去AC即可;
②先利用AB的长度算出Q比P晚出发的时间,再利用P和Q运动总路程等于两个AC的长度列方程即可.
解:(1)由数轴可知:AC=10-(﹣26)=36个单位长度
∵动点P从A出发,以每秒1个单位的速度向终点C移动
PA=t,PC=36-t;
(2)①由数轴可知:BC=10-(﹣10)=20个单位长度,

∴P从B运动到C的时间为:20÷1=20s
∵当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动
∴当P从B运动到C时,Q的运动时间也是20s
∴Q的运动路程为:20×3=60个单位长度,
∵此时P在C处
∴QP=QC=60-AC=60-36=24.
②由数轴可知:AB=(﹣10)-(﹣26)=16个单位长度,

∵当点P运动到B点时,点Q从A点出发,
∴Q比P晚出发了:16÷1=16s
故Q的运动时间为(t-16)s,
由图可知:P和Q运动总路程等于两个AC的长度
∴t+3(t-16)=2×36
解得:t=30
答:当t等于30时,P、Q两点恰好在途中相遇
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索规律:将连续的偶数2,4,6,8,…,排列如下表:
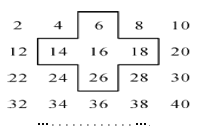
(1)十字框中的五个数的和与中间的数16有什么关系?
(2)若将十字框上下左右移动,可框住另外的五个数,其他五个数的和能等于2010吗?如能,写出这五个数,如不能,说明理由.
-
科目: 来源: 题型:
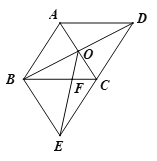
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC,BD相交于点O,∠ABC=60°,过点B作AC的平行线交DC的延长线于点E.
(1) 求证:四边形ABEC为菱形;
(2) 若AB=6,连接OE,求OE的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ ACB=115O,BD=BC,AE=AC. 则∠ECD的度数为_________.
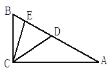
-
科目: 来源: 题型:
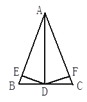
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别是E、F,则下列四个结论: (1) DE=DF; (2) AD上任一点到点C、点B的距离相等; (3) BD=CD,AD⊥BC;(4)∠BDE=∠CDF,其中,正确的有__________个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,AC为直径,=,DE⊥BC,垂足为E.

(1)求证:CD平分∠ACE;
(2)判断直线ED与⊙O的位置关系,并说明理由;
(3)若CE=1,AC=4,求阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知表②,表③分别是从表①中选取的一部分,表①中第一行第四个数是3,第二行第三个数是5,根据表①中的规律,解答下列问题:
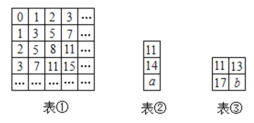
(1)表①中第四行第五个数是_____;
(2)表②,表③中的
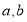 的和是_____;
的和是_____;(3)①求第四行第几个数是107?
②表①中第
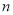 行第7个数是_____(用含
行第7个数是_____(用含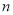 的式子表示);
的式子表示);(4)表①中第
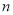 行第
行第 个数是_____(用含
个数是_____(用含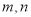 的式子表示)
的式子表示)
相关试题

