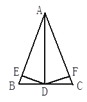
【题目】如图,在△ABC中,∠ ACB=115O,BD=BC,AE=AC. 则∠ECD的度数为_________.
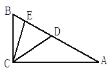
参考答案:
【答案】32.5°.
【解析】
根据等腰三角形的性质可设∠AEC=∠ACE=x°、∠BDC=∠BCD=y°,即可得∠A=180°-2x°,∠B=180°-2y°,由三角形的内角和定理可得115+(180-2x)+(180-2y)=180,解方程可得x+y=147.5,由此即可求得∠ECD的度数.
∵AC=AE,BC=BD,
∴设∠AEC=∠ACE=x°,∠BDC=∠BCD=y°,
∴∠A=180°-2x°,∠B=180°-2y°,
∵∠ACB+∠A+∠B=180°,
∴115+(180-2x)+(180-2y)=180,
∴x+y=147.5,
∴∠DCE=180-(∠AEC+∠BDC)=180-(x+y)=32.5°.
故答案为:32.5°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在钝角三角形ABC中,把AB=AC,D是BC上一点,AD把
 ABC分成两个等腰三角形,则
ABC分成两个等腰三角形,则 BAC的度数为( )
BAC的度数为( )A.
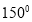 B.
B. 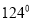 C.
C. 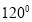 D.
D. 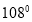
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索规律:将连续的偶数2,4,6,8,…,排列如下表:
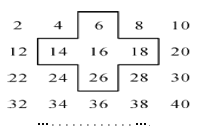
(1)十字框中的五个数的和与中间的数16有什么关系?
(2)若将十字框上下左右移动,可框住另外的五个数,其他五个数的和能等于2010吗?如能,写出这五个数,如不能,说明理由.
-
科目: 来源: 题型:
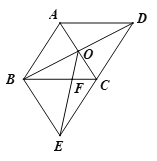
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC,BD相交于点O,∠ABC=60°,过点B作AC的平行线交DC的延长线于点E.
(1) 求证:四边形ABEC为菱形;
(2) 若AB=6,连接OE,求OE的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有A. B.C三点,分别表示有理数26,10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设点P移动时间为t秒。

(1)PA= ,PC= (用含t的代数式表示)
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,当点P运动到点C时,P、Q两点运动停止,
①当P、Q两点运动停止时,求点P和点Q的距离;
②求当t为何值时P、Q两点恰好在途中相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别是E、F,则下列四个结论: (1) DE=DF; (2) AD上任一点到点C、点B的距离相等; (3) BD=CD,AD⊥BC;(4)∠BDE=∠CDF,其中,正确的有__________个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,AC为直径,=,DE⊥BC,垂足为E.

(1)求证:CD平分∠ACE;
(2)判断直线ED与⊙O的位置关系,并说明理由;
(3)若CE=1,AC=4,求阴影部分的面积.
相关试题

