【题目】点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.
利用数轴,根据数形结合思想,回答下列问题:
![]()
(1)已知|x|=3,则x的值是 .
(2)数轴上表示2和6两点之间的距离是 ,数轴上表示1和﹣2的两点之间的距离为 ;
(3)数轴上表示x和1两点之间的距离为 ,数轴上表示x和﹣3两点之间的距离为
(4)若x表示一个实数,且﹣5<x<3,化简|x﹣3|+|x+5|= ;
(5)|x+3|+|x﹣4|的最小值为 ,|x﹣1|+|x﹣2|+|x﹣3|+|x﹣4|+|x﹣5|的最小值为 .
(6)|x+1|﹣|x﹣3|的最大值为 .
参考答案:
【答案】(1)![]() ;(2)4, 3;(3)|x﹣1|,|x+3|;(4)8;(5)7,6;(6)4.
;(2)4, 3;(3)|x﹣1|,|x+3|;(4)8;(5)7,6;(6)4.
【解析】
(1)根据绝对值的意义,即可得到答案;
(2)(3)直接代入公式即可;
(4)实质是在表示3和-5的点之间取一点,计算该点到点3和-5的距离和;
(5)可知x对应点在对应-3和4的点之间时|x+3|+|x-4|的值最小;x对应点在3时,|x-1|+|x-2|+|x-3|+|x-4|+|x-5|值最小;
(6)可知x对应点在表示-1和3的点所形成的线段外时,|x+1|-|x-3|的值最大.
解:(1)∵![]() ,则
,则![]() ;
;
故答案为:![]() ;
;
(2)![]() ,
,![]() ,
,
故答案为:4,3;
(3)根据两点间距离公式可知:数轴上表示x和1两点之间的距离为:![]() ;
;
数轴上表示x和-3两点之间的距离为:![]() ;
;
故答案为:![]() ,
,![]() ;
;
(4)x对应点在点-5和3之间时的任意一点时|x-3|+|x+5|的值都是8;
故答案为:8;
(5)x对应点在点-4和3之间时的任意一点,|x-3|+|x+4|的值最小是7;
当x对应点是3时,|x-1|+|x-2|+|x-3|+|x-4|+|x-5|的最小值为6;
故答案为:7,6;
(6)当x对应点不在-1和3对应点所在的线段上,即x<-1或x>3时,
|x+1|-|x-3|的最大值为4;
故答案为:4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年3月27日是全国中小学生安全教育日,某校为加强学生的安全意识,组织了全校学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整致,满分为10分) 进行统计,绘制了图中两幅不完整的统计图.

(1)a=_____,n=_____;
(2)补全频数直方图;
(3)该校共有2000名学生.若成绩在70分以下(含70分)的学生安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于20%(不考虑其它因素),那么每个机器人的标价至少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD中,点E、F分别在边CD、AB上,且DE=BF,∠ECA=∠FCA.
(1)求证:四边形AFCE是菱形;
(2)若AB=8,BC=4,求菱形AFCE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学有一块四边形的空地ABCD,如图所示,经测量∠A=90°,AB=6m,BC=24m,CD=26m,DA=8m.
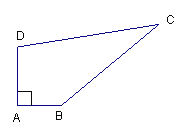
(1)求四边形ABCD的面积;
(2)学校计划在空地上种植草皮,若每平方米草皮需要200元,问学校需要投入多少资金买草皮
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,过点O作两条射线OM、ON,且∠AOM=∠CON=90°

(1)若OC平分∠AOM,求∠AOD的度数.
(2)若∠1=
 ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD. -
科目: 来源: 题型:
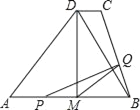
查看答案和解析>>【题目】如图,M为等腰△ABD的底AB的中点,过D作DC∥AB,连结BC;AB=8cm,DM=4cm,DC=1cm,动点P自A点出发,在AB上匀速运动,动点Q自点B出发,在折线BC﹣CD上匀速运动,速度均为1cm/s,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(s)时,△MPQ的面积为S(不能构成△MPQ的动点除外).
(1)t(s)为何值时,点Q在BC上运动,t(s)为何值时,点Q在CD上运动;
(2)求S与t之间的函数关系式;
(3)当t为何值时,S有最大值,最大值是多少?
(4)当点Q在CD上运动时,直接写出t为何值时,△MPQ是等腰三角形.
相关试题

