【题目】如图,△ABC中,∠ACB=90°,∠ABC=25°,以点C为旋转中心顺时针旋转后得到△A′B′C,且点A在边A′B′上,则旋转角的度数为( )

A. 65°B. 60°C. 50°D. 40°
参考答案:
【答案】C
【解析】
先利用互余计算出∠BAC=65°,再利用旋转的性质得CA=CA′,∠A′=∠A′AC=65°,∠ACA′等于旋转角,根据等腰三角形的性质和三角形内角和计算出∠ACA′的度数即可.
解:∵∠ACB=90°,∠ABC=25°,
∴∠BAC=65°,
∵以点C为旋转中心顺时针旋转后得到△A′B′C,且点A在边A′B′上,
∴CA=CA′,∠A′=∠BAC=65°,∠ACA′等于旋转角,
∴∠CAA′=∠A′=65°,
∴∠ACA′=180°﹣65°﹣65°=50°,
即旋转角的度数为50°.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,
 ,
, 分别在直线
分别在直线 上,
上, 是平面内一点,
是平面内一点, 和
和 的平分线所在直线相交于点
的平分线所在直线相交于点 .
.(1)如图1,当
 都在直线
都在直线 之间,且
之间,且 时,
时, 的度数为_________;
的度数为_________;(2)如图2,当
 都在直线
都在直线 上方时,探究
上方时,探究 和
和 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;(3)如图3,当
 在直线
在直线 两侧时,直接写出
两侧时,直接写出 和
和 之间的数量关系是_____.
之间的数量关系是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠CAB=2∠B,AE平分∠CAB,CD⊥AB于D,AC=3,AD=1.下列结论:①∠AEC=∠CAB;②EF=CE;③AC=AE;④BD=4;

正确的是___________(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于
 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
A. 2 B. 4 C. 6 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是( )
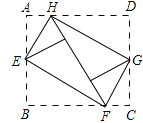
A. 12厘米 B. 16厘米 C. 20厘米 D. 28厘米
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生整体的数学学习能力,年级组织了“数学钻石活动”,从中随机抽取部分学生的成绩进行统计分析,整理得到如下不完整的频数分布表和数分布直方图:


(1)表中的
 ,
, ;
;(2)把上面的频数分布直方图补充完整;
(3)根据调查结果,估计年级500名学生中,成绩不低于85分的人数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD与矩形EFGH在直线
 的同侧,边AD,EH在直线
的同侧,边AD,EH在直线 上,且AD=5 cm,EH=4 cm, EF=3 cm.保持正方形ABCD不动,将矩形EFGH沿直线
上,且AD=5 cm,EH=4 cm, EF=3 cm.保持正方形ABCD不动,将矩形EFGH沿直线 左右移动,连接BF、CG,则BF+CG的最小值为( )
左右移动,连接BF、CG,则BF+CG的最小值为( ) 
A. 4B.
 C.
C.  D. 5
D. 5
相关试题

