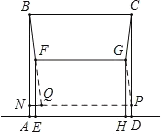
【题目】如图,正方形ABCD与矩形EFGH在直线![]() 的同侧,边AD,EH在直线
的同侧,边AD,EH在直线![]() 上,且AD=5 cm,EH=4 cm, EF=3 cm.保持正方形ABCD不动,将矩形EFGH沿直线
上,且AD=5 cm,EH=4 cm, EF=3 cm.保持正方形ABCD不动,将矩形EFGH沿直线![]() 左右移动,连接BF、CG,则BF+CG的最小值为( )
左右移动,连接BF、CG,则BF+CG的最小值为( )

A. 4B. ![]() C.
C. ![]() D. 5
D. 5
参考答案:
【答案】B
【解析】
作点C关于FG的对称点P,连接GP,以FG,PG为邻边作平行四边形PGFQ,则BF+CG=BF+QF,当B,F,Q三点共线时,BF+CG的最小值为BQ的长,过点Q作QN⊥AB于N,依据勾股定理即可得到在Rt△BNQ中,BQ=![]() ,即可得出BF+CG的最小值为
,即可得出BF+CG的最小值为![]() .
.
解:如图所示,作点C关于FG的对称点P,连接GP,
以FG,PG为邻边作平行四边形PGFQ,则FQ=PG=CG,FG=QP=4,
∴BF+CG=BF+QF,
∴当B,F,Q三点共线时,BF+CG的最小值为BQ的长,
过点Q作QN⊥AB于N,
由题可得BN=2(53)=4,NQ=54=1,
∴Rt△BNQ中,BQ=![]() ,
,
∴BF+CG的最小值为![]() ,
,
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,∠ABC=25°,以点C为旋转中心顺时针旋转后得到△A′B′C,且点A在边A′B′上,则旋转角的度数为( )

A. 65°B. 60°C. 50°D. 40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是( )
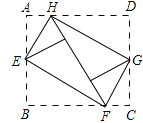
A. 12厘米 B. 16厘米 C. 20厘米 D. 28厘米
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生整体的数学学习能力,年级组织了“数学钻石活动”,从中随机抽取部分学生的成绩进行统计分析,整理得到如下不完整的频数分布表和数分布直方图:


(1)表中的
 ,
, ;
;(2)把上面的频数分布直方图补充完整;
(3)根据调查结果,估计年级500名学生中,成绩不低于85分的人数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形
 中,对角线
中,对角线 与
与 相交于点
相交于点 .要使四边形
.要使四边形 是正方形,还需添加一组条件.下面给出了五组条件:①
是正方形,还需添加一组条件.下面给出了五组条件:① ,且
,且 ;②
;② , 且
, 且 ;③
;③ ,且
,且 ;④
;④ ,且
,且 ;⑤
;⑤ ,且
,且 .其中正确的是________(填写序号).
.其中正确的是________(填写序号). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, 为
为 边上的中线,
边上的中线, ∥
∥ ,且
,且 ,连接
,连接 .
.(1)求证:四边形
 为菱形;
为菱形;(2)连接
 ,若
,若 平分
平分 ,
, ,求
,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在等边△ABC中, AB=
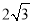 , D,E分别是AB,BC的中点(如图).若将△BDE绕点B逆时针旋转,得到△BD1E1,设旋转角为α(0°<α<180°),记射线CE1与AD1的交点为P.点P到BC所在直线的距离的最大值为_____________.
, D,E分别是AB,BC的中点(如图).若将△BDE绕点B逆时针旋转,得到△BD1E1,设旋转角为α(0°<α<180°),记射线CE1与AD1的交点为P.点P到BC所在直线的距离的最大值为_____________.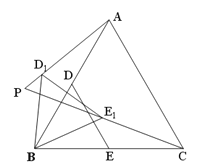
相关试题

