【题目】如图,一次函数y=k1x+b(k1≠0)与反比例函数![]() 的图象交于点A(-1,2),B(m,-1).
的图象交于点A(-1,2),B(m,-1).
(1)求一次函数与反比例函数的解析式;
(2)在x轴上是否存在点P(n,0),使△ABP为等腰三角形,请你直接写出P点的坐标.

参考答案:
【答案】(1)反比例函数的解析式为![]() ;一次函数的解析式为y=-x+1;(2)满足条件的P点的坐标为(-1+
;一次函数的解析式为y=-x+1;(2)满足条件的P点的坐标为(-1+![]() ,0)或(-1-
,0)或(-1-![]() ,0)或(2+
,0)或(2+![]() ,0)或(2-
,0)或(2-![]() ,0)或(0,0).
,0)或(0,0).
【解析】
(1)将A点代入求出k2,从而求出反比例函数方程,再联立将B点代入即可求出一次函数方程.
(2)令PA=PB,求出P.令AP=AB,求P.令BP=BA,求P.根据坐标距离公式计算即可.
(1)把A(-1,2)代入![]() ,得到k2=-2,
,得到k2=-2,
∴反比例函数的解析式为![]() .
.
∵B(m,-1)在![]() 上,∴m=2,
上,∴m=2,
由题意![]() ,解得:
,解得:![]() ,∴一次函数的解析式为y=-x+1.
,∴一次函数的解析式为y=-x+1.
(2)满足条件的P点的坐标为(-1+![]() ,0)或(-1-
,0)或(-1-![]() ,0)或(2+
,0)或(2+![]() ,0)或(2-
,0)或(2-![]() ,0)或(0,0).
,0)或(0,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(2
 ,2)、B(2
,2)、B(2  ,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(﹣2
,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(﹣2  ,2
,2  )的位置,则图中阴影部分的面积为 .
)的位置,则图中阴影部分的面积为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若四边形ABCD、四边形GFED都是正方形,AD=4,
 ,当正方形GFED绕D旋转到如图的位置,点F在边AD上,延长CE交AG于H,交AD于M.则CM的长为 .
,当正方形GFED绕D旋转到如图的位置,点F在边AD上,延长CE交AG于H,交AD于M.则CM的长为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点A(a,0),B(0,b),且a、b满足
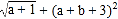 =0, □ABCD的边AD与y轴交于点E(0,2),且E为AD中点,双曲线
=0, □ABCD的边AD与y轴交于点E(0,2),且E为AD中点,双曲线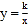 经过C、D两点.
经过C、D两点. (1)求k的值;
(2)点P在双曲线
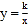 上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;(3)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时,
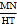 的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.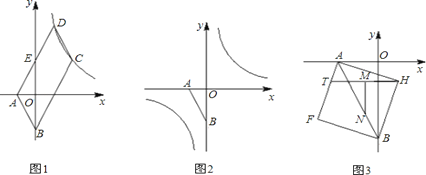
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司开发处一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.

(1)求y与x之间的函数表达式,并写出x的取值范围;
(2)若该节能产品的日销售利润为W(元),求W与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第几天的日销售利润最大,最大日销售利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+4x﹣k=0有两个不相等的实数根.
(1)求k的取值范围;
(2)请你在﹣5,﹣4,﹣3,1,2,3中选择一个数作为k的值,使方程有两个整数根,并求出方程的两个整数根. -
科目: 来源: 题型:
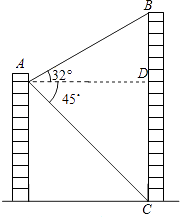
查看答案和解析>>【题目】如图,从一个建筑物的A处测得对面楼BC的顶部B的仰角为32°,底部C的俯角为45°,观测点与楼的水平距离AD为31m,楼BC的高度大约为多少?(结果取整数).(参考数据:sin32°≈0.5,cos32°≈0.8,tan32°≈0.6)
相关试题

