【题目】已知关于x的一元二次方程x2+4x﹣k=0有两个不相等的实数根.
(1)求k的取值范围;
(2)请你在﹣5,﹣4,﹣3,1,2,3中选择一个数作为k的值,使方程有两个整数根,并求出方程的两个整数根.
参考答案:
【答案】
(1)
解:∵方程x2+4x﹣k=0有两个不相等的实数根,
∴△=42﹣4×1×(﹣k)=16+4k>0,
解得:k>﹣4,
∴k的取值范围为k>﹣4;
(2)
解:当k=﹣3时,△=16+4k=4,
原方程为x2+4x+3=(x+1)(x+3)=0,
解得:x=﹣1或x=﹣3;
当k=1时,△=16+4k=20,
![]() 不是整数;
不是整数;
当k=2时,△=16+4k=24,
![]() 不是整数;
不是整数;
当k=3时,△=16+4k=28,
![]() 不是整数.
不是整数.
∴当取k=﹣3时,方程的两个整数根为﹣1或﹣3.
【解析】(1)根据方程有两个不等实根结合根的判别式,可得出关于k的一元一次不等式,解不等式即可得出k的取值范围;(2)结合(1)的结论,找出k的值,并验证k为这些数时,何时方程的两根为整数,由此即可得出结论.
【考点精析】解答此题的关键在于理解求根公式的相关知识,掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点A(a,0),B(0,b),且a、b满足
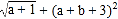 =0, □ABCD的边AD与y轴交于点E(0,2),且E为AD中点,双曲线
=0, □ABCD的边AD与y轴交于点E(0,2),且E为AD中点,双曲线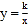 经过C、D两点.
经过C、D两点. (1)求k的值;
(2)点P在双曲线
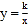 上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;(3)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时,
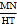 的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.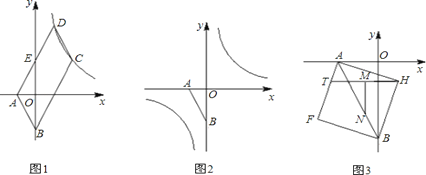
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=k1x+b(k1≠0)与反比例函数
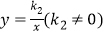 的图象交于点A(-1,2),B(m,-1).
的图象交于点A(-1,2),B(m,-1).(1)求一次函数与反比例函数的解析式;
(2)在x轴上是否存在点P(n,0),使△ABP为等腰三角形,请你直接写出P点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司开发处一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.

(1)求y与x之间的函数表达式,并写出x的取值范围;
(2)若该节能产品的日销售利润为W(元),求W与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第几天的日销售利润最大,最大日销售利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从一个建筑物的A处测得对面楼BC的顶部B的仰角为32°,底部C的俯角为45°,观测点与楼的水平距离AD为31m,楼BC的高度大约为多少?(结果取整数).(参考数据:sin32°≈0.5,cos32°≈0.8,tan32°≈0.6)
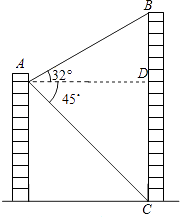
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥DC,AD∥BC,BE=DF,则图中全等的三角形有( )
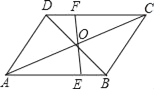
A. 3对 B. 4对 C. 5对 D. 6对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ADB=∠ACB=90°,AC与BD交于点O,且AC=BD.有下列结论:①AD=BC;②∠DBC=∠CAD;③AO=BO;④AB∥CD.其中正确的是( )
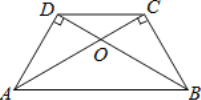
A. ①②③④ B. ①②③ C. ①②④ D. ②③④
相关试题

