【题目】已知:如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 的延长线于
的延长线于![]() ,连接
,连接![]() 并延长交
并延长交![]() 的延长线于
的延长线于![]() .
.
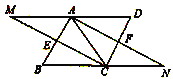
(1)求证:![]() ;
;
(2)当平行四边形![]() 中
中![]() 等于多少度时,四边形
等于多少度时,四边形![]() 是正方形?请说明理由.
是正方形?请说明理由.
参考答案:
【答案】(1)见解析(2)当![]() =45°时,四边形
=45°时,四边形![]() 是正方形,理由见解析
是正方形,理由见解析
【解析】
(1)根据平行四边形得到AB=CD,AB∥CD,∠B=∠D,根据线段中点的定义得到AE=![]() AB,CF=
AB,CF=![]() CD,推出四边形AECF是平行四边形,得到四边形AECF是矩形,根据全等三角形的判定定理得到结论;
CD,推出四边形AECF是平行四边形,得到四边形AECF是矩形,根据全等三角形的判定定理得到结论;
(2)当![]() =45°时,可得CE⊥AB,AE=EC,故可得到四边形
=45°时,可得CE⊥AB,AE=EC,故可得到四边形![]() 是正方形.
是正方形.
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,∠B=∠D,
∵E,F分别是AB,CD的中点,
∴AE=![]() AB,CF=
AB,CF=![]() CD,
CD,
∴AE=CF,
∵AE∥CF,
∴四边形AECF是平行四边形,
∵AC=CB,
∴CE⊥AB,
∴∠AEC=90°,
∴四边形AECF是矩形,
∴∠BAN=∠DCM=90°,
在△ABN与△CDM中,
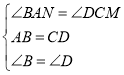 ,
,
∴△ABN≌△CDM(ASA);
(2)解:当∠B=45°时,四边形AECF是正方形,
理由:∵BC=AC,
∴∠B=∠BAC=45°,
∵E是AB的中点,
∴CE⊥AB,
∴AE=EC,
∴矩形AECF是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点
 是直线
是直线 上第一象限的点,点
上第一象限的点,点 的坐标是
的坐标是 ,
, 是坐标原点,
是坐标原点, 的面积为
的面积为 ,则
,则 关于
关于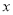 的函数关系式(取值范围)是__________.
的函数关系式(取值范围)是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.
(1)求证:AB∥CD;
(2)求∠C的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学举行十佳歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
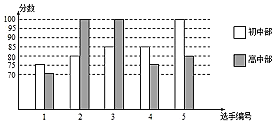
(1)根据所给信息填空:
平均数(分)
中位数(分)
众数(分)
方差
初中部
85
______
85
_______
高中部
_____
80
______
160
(2)你觉得高中部和初中部的决赛成绩哪个更好?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,AB=CD,点E,F在BC上,且BE=CF.

(1)求证:△ABE≌△DCF;
(2)试证明:以A,F,D,E为顶点的四边形是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】三个互不相等的有理数,既可以表示为0,b,
 的形式,也可以表示为1,a,a+b的形式,那么a=_______;b=_________.
的形式,也可以表示为1,a,a+b的形式,那么a=_______;b=_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形
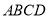 中,
中, ,
, ,
, 是
是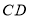 上的点,
上的点, 交
交 于点
于点 ,连接
,连接 .
.
(1)求证:
 ;
;(2)若
 ,试证明:四边形
,试证明:四边形 是菱形;
是菱形;(3)在(2)的条件下,已知
 ,求证:
,求证: .
.
相关试题

