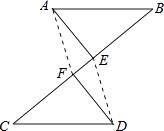
【题目】如图,AB∥CD,AB=CD,点E,F在BC上,且BE=CF.
(1)求证:△ABE≌△DCF;
(2)试证明:以A,F,D,E为顶点的四边形是平行四边形.
参考答案:
【答案】
(1)证明:如图,∵AB∥CD,
∴∠B=∠C.
∵在△ABE与△DCF中,
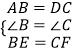 ,
,
∴△ABE≌△DCF(SAS)
(2)证明:如图,连接AF、DE.
由(1)知,△ABE≌△DCF,
∴AE=DF,∠AEB=∠DFC,
∴∠AEF=∠DFE,
∴AE∥DF,
∴以A、F、D、E为顶点的四边形是平行四边形.
【解析】(1)要证明△ABE≌△DCF,题中已知这两个三角形中两组对应边相等,还差一条件,要么证明第三组对应边相等,或证已知两组对应边的夹角相等,根据已知AB∥CD,可证得已知两组对应边的夹角相等,即可证明两三角形全等。
(2)根据(1)中易证得△ABE≌△DCF,可证明到AE平行且等于DF。继而可证得以A、F、D、E为顶点的四边形是平行四边形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.
(1)求证:AB∥CD;
(2)求∠C的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学举行十佳歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
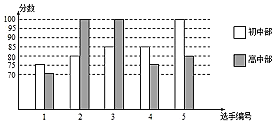
(1)根据所给信息填空:
平均数(分)
中位数(分)
众数(分)
方差
初中部
85
______
85
_______
高中部
_____
80
______
160
(2)你觉得高中部和初中部的决赛成绩哪个更好?说明理由.
-
科目: 来源: 题型:
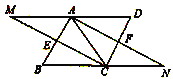
查看答案和解析>>【题目】已知:如图,在平行四边形
 中,
中,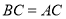 ,
,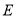 ,
,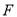 分别是
分别是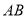 ,
,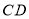 的中点,连接
的中点,连接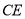 并延长交
并延长交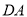 的延长线于
的延长线于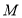 ,连接
,连接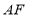 并延长交
并延长交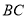 的延长线于
的延长线于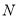 .
.
(1)求证:
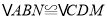 ;
;(2)当平行四边形
 中
中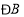 等于多少度时,四边形
等于多少度时,四边形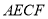 是正方形?请说明理由.
是正方形?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】三个互不相等的有理数,既可以表示为0,b,
 的形式,也可以表示为1,a,a+b的形式,那么a=_______;b=_________.
的形式,也可以表示为1,a,a+b的形式,那么a=_______;b=_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形
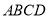 中,
中, ,
, ,
, 是
是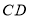 上的点,
上的点, 交
交 于点
于点 ,连接
,连接 .
.
(1)求证:
 ;
;(2)若
 ,试证明:四边形
,试证明:四边形 是菱形;
是菱形;(3)在(2)的条件下,已知
 ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,各地“广场舞”噪音干扰的问题备受关注,相关人员对本地区15﹣65岁年龄段的500名市民进行了随机调查,在调查过程中对“广场舞”噪音干扰的态度有以下五种:A:没影响;B:影响不大;C:有影响,建议做无声运动,D:影响很大,建议取缔;E:不关心这个问题,将调查结果绘统计整理并绘制成如下两幅不完整的统计图.

请根据以上信息解答下列问题:
(1)填空m= , 态度为C所对应的圆心角的度数为;
(2)补全条形统计图;
(3)若全区15﹣65岁年龄段有20万人,估计该地区对“广场舞”噪音干扰的态度为B的市民人数;
(4)若在这次调查的市民中,从态度为A的市民中抽取一人的年龄恰好在年龄段15﹣35岁的概率是多少?
相关试题

