【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上的点,
上的点,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.

(1)求证:![]() ;
;
(2)若![]() ,试证明:四边形
,试证明:四边形![]() 是菱形;
是菱形;
(3)在(2)的条件下,已知![]() ,求证:
,求证:![]() .
.
参考答案:
【答案】(1)见解析(2)见解析(3)见解析
【解析】
(1)先判断出△ABC≌△ADC即可得到∠BAF=∠DAC,再判断出△ABF≌△ADF得出∠AFB=∠AFD,即可得到![]() ;
;
(2)先由平行得到角相等,用等量代换得出∠DAC=∠ACD,最后判断出四边相等;
(3)由(2)得到判断出△BCF≌△DCF,结合BE⊥CD即可求解.
(1)在△ABC和△ADC中
 ,
,
∴△ABC≌△ADC,
∴∠BAC=∠DAC,
在△ABF和△ADF中
 ,
,
∴△ABF≌△ADF,
∴![]() ;
;
(2)∵AB∥CD,
∴∠BAC=∠ACD,
∵∠BAC=∠DAC,
∴∠DAC=∠ACD,
∴AD=CD,
∵AB=AD,CB=CD,
∴AB=CB=CD=AD,
∴四边形ABCD是菱形;
(3)∵四边形ABCD是菱形,
∴BC=CD,∠BCF=∠DCF,
∵CF=CF,
∴△BCF≌△DCF,
∴∠CBF=∠CDF,
∵BE⊥CD,
∴∠BEC=∠DEF=90![]() ,
,
∴∠BCD+∠CBF=∠EFD+∠CDF =90![]()
∴![]() .
.
-
科目: 来源: 题型:
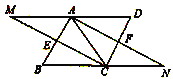
查看答案和解析>>【题目】已知:如图,在平行四边形
 中,
中,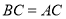 ,
,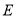 ,
,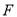 分别是
分别是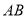 ,
,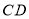 的中点,连接
的中点,连接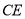 并延长交
并延长交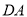 的延长线于
的延长线于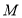 ,连接
,连接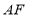 并延长交
并延长交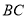 的延长线于
的延长线于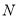 .
.
(1)求证:
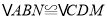 ;
;(2)当平行四边形
 中
中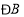 等于多少度时,四边形
等于多少度时,四边形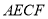 是正方形?请说明理由.
是正方形?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,AB=CD,点E,F在BC上,且BE=CF.

(1)求证:△ABE≌△DCF;
(2)试证明:以A,F,D,E为顶点的四边形是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】三个互不相等的有理数,既可以表示为0,b,
 的形式,也可以表示为1,a,a+b的形式,那么a=_______;b=_________.
的形式,也可以表示为1,a,a+b的形式,那么a=_______;b=_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,各地“广场舞”噪音干扰的问题备受关注,相关人员对本地区15﹣65岁年龄段的500名市民进行了随机调查,在调查过程中对“广场舞”噪音干扰的态度有以下五种:A:没影响;B:影响不大;C:有影响,建议做无声运动,D:影响很大,建议取缔;E:不关心这个问题,将调查结果绘统计整理并绘制成如下两幅不完整的统计图.

请根据以上信息解答下列问题:
(1)填空m= , 态度为C所对应的圆心角的度数为;
(2)补全条形统计图;
(3)若全区15﹣65岁年龄段有20万人,估计该地区对“广场舞”噪音干扰的态度为B的市民人数;
(4)若在这次调查的市民中,从态度为A的市民中抽取一人的年龄恰好在年龄段15﹣35岁的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中有大小不同的平行四边形,第一幅图中有1个平行四边形,第二幅图中有3个平行四边形,第三幅图中有5个平行四边形,则第6幅和第7幅图中合计有( )个平行四边形

A.22B.24C.26D.28
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
第1个等式:a1=
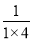 =
=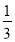 ×(
×(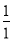 ﹣
﹣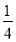 );
);第2个等式:a2=
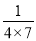 =
=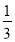 ×(
×(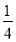 ﹣
﹣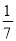 );
);第3个等式:a3=
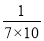 =
=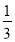 ×(
×(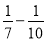 );
);第4个等式:a4=
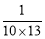 =
=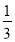 ×(
×(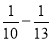 );
);…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= = ;第n(n为正整数)个等式:an= = ;
(2)求a1+a2+a3+a4+…+a100的值;
(3)数学符号
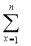 f(x)=f(1)+f(2)+f(3)+…+f(n),试求
f(x)=f(1)+f(2)+f(3)+…+f(n),试求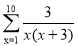 的值.
的值.
相关试题

