【题目】已知A(1,0)、B(0,-1)、C(-1,2)、D(2,-1)、E(4,2)五个点,抛物线y=a(x-1)2+k(a>0)经过其中的三个点.
(1)求证:C、E两点不可能同时在抛物线y=a(x-1)2+k(a>0)上;
(2)点A在抛物线y=a(x-1)2+k(a>0)上吗?为什么?
(3)求a和k的值.
参考答案:
【答案】
(1)
解:∵抛物线y=a(x-1)2+k的对称轴为x=1,
而C(-1,2),E(4,2)两点纵坐标相等,
由抛物线的对称性可知,C、E关于直线x=1对称,
又∵C(-1,2)与对称轴相距2,E(4,2)与对称轴相距3,
∴C、E两点不可能同时在抛物线上;
(2)
解:假设点A(1,0)在抛物线y=a(x-1)2+k(a>0)上,
则a(1-1)2+k=0,解得k=0,
因为抛物线经过5个点中的三个点,
将B(0,-1)、C(-1,2)、D(2,-1)、E(4,2)代入,
得出a的值分别为a=-1,a= ![]() ,a=-1,a=
,a=-1,a= ![]() ,
,
所以抛物线经过的点是B,D,
又因为a>0,与a=-1矛盾,
所以假设不成立.
所以A不在抛物线上;
而k为任意数,这与抛物线是确定的矛盾,故点A不在抛物线y=a(x-1)2+k(a>0)上.
∴A点不在抛物线上
(3)
解:将D(2,-1)、C(-1,2)两点坐标代入y=a(x-1)2+k中,得
![]() 解得
解得![]()
或将E、D两点坐标代入y=a(x-1)2+k中,得 |
![]() 解得
解得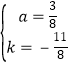
综上所述,
![]()
或 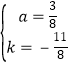
【解析】本题考查了二次函数图象上点的坐标特点.关键是明确图象上点的坐标必须满足函数解析式.(1)由抛物线y=a(x-1)2+k可知,抛物线对称轴为x=1,而C(-1,2),E(4,2)两点纵坐标相等,应该关于直线x=1对称,但C(-1,2)与对称轴相距2,E(4,2)与对称轴相距3,故不可能;(2)假设A点在抛物线上,得出矛盾排除A点在抛物线上;(3)B、D两点关于对称轴x=1对称,一定在抛物线上,另外一点可能是C点或E点,分别将C、D或D、E两点坐标代入求a和k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中,  ,
,  ,点
,点 在
在 的延长线上,
的延长线上,  是
是 的中点,
的中点,  是射线
是射线 上一动点,且
上一动点,且 ,连接
,连接 ,作
,作 ,
,  交
交 延长线于点
延长线于点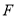 .
.(
 )如图
)如图 ,当点
,当点 在
在 上时,填空:
上时,填空:  __________
__________ 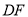 (填“
(填“ ”、“
”、“ ”或“
”或“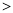 ”).
”).(
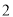 )如图
)如图 ,当点
,当点 在
在 的延长线上时,请根据题意将图形补全,判断
的延长线上时,请根据题意将图形补全,判断 与
与 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题:
定义:如果一个数的平方等于﹣1,记为i2=﹣1,这个数i叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为a+bi(a,b为实数),a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算:(2+i)+(3﹣4i)=5﹣3i.
(1)填空:i4= ,i5= .
(2)计算:①(4+i)(4﹣i); ②(3+i)2;
(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:已知:(x+y)+3i=(1﹣x)﹣yi,(x,y为实数),求x,y的值.
(4)试一试:请利用以前学习的有关知识将
 化简成a+bi的形式.
化简成a+bi的形式. -
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接“五一劳动节”,某超市开展促销活动,决定对A,B两种商品进行打折出售.打折前,买6件A商品和3件B商品需要108元,买3件A商品和4件B商品需要94元.问:打折后,若买5件A商品和4件B商品仅需86元,比打折前节省了多少元钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BC边的垂直平分线交AC边于点D,连接BD.
(1)如图CE=4,△BDC的周长为18,求BD的长.
(2)求∠ADM=60°,∠ABD=20°,求∠A的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某物流公司承接A、B两种货物运输业务,已知3月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收取运费9500元;4月份由于工人工资上涨,运费单价上涨情况为:A货物运费单价增加了40%,B货物运费单价上涨到40元/吨;该物流公司4月承接的A种货物和B种货物的数量与3月份相同,4月份共收取运费13000元.试求该物流公司3月份运输A、B两种货物各多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】广州火车南站广场计划在广场内种植A,B两种花木共 6600棵,若A花木数量是B花木数量的2倍少600棵.
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
相关试题

