【题目】如图,数轴上的点A,B,C,D,E表示连续的五个整数,对应的数分别为a,b,c,d,e.
(1)若a=-3,则e = ;
(2)若a+e=0,则代数式b+c+d= ;
(3)若d是最大的负整数,求代数式![]() 的值(写出求解过程).
的值(写出求解过程).
(4)若e=4,F也为数轴上一点,且BE=2FE,则F表示的数为 ;
![]()
参考答案:
【答案】(1)1; (2) 0; (3)0; (4) 2.5或5.5.
【解析】
(1)根据数轴的特点,即可得解;
(2)根据已知条件,可判定A和E、B和D到C的距离相等,则可得解;
(3)首先判定出d=-1,则a、b、c、e便可得知,进而得解;
(4)根据已知条件,可得出BE,即可得解.
(1)∵a=-3,a,b,c,d,e表示连续的五个整数
∴e =1
(2)∵a+e=0,
∴A和E、B和D到C的距离相等,
∴b+c+d=0
(3)根据题意,得d=-1
∴a=-4,b=-3,c=-2,e=0
∴![]() =
=![]() =0
=0
(4)根据已知条件,得BE=3
∵BE=2FE,
∴FE=1.5
∵E表示的数是4
∴若F在E的左边,则F表示的数是2.5;
若F在E的右边,则F表示的数是5.5;
∴F表示的数为2.5或5.5
-
科目: 来源: 题型:
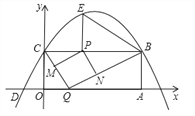
查看答案和解析>>【题目】如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).
(1)请直接写出B、C两点的坐标及抛物线的解析式;
(2)过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE=∠OCD?
(3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,请求出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD的轨道上有两个点甲与乙,开始时甲在A处,乙在C处,它们沿着正方形轨道顺时针同时出发,甲的速度为每秒1cm,乙的速度为每秒5cm,已知正方形轨道ABCD的边长为2cm,则乙在第2019次追上甲时的位置在( )
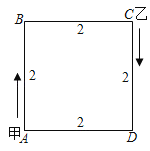
A.AB上B.BC上C.CD上D.AD上
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,面积为28的平行四边形纸片ABCD中,AB=7,∠BAD=45°,按下列步骤进行裁剪和拼图.

第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△ABD和△BCD纸片,再将△ABD纸片沿AE剪开(E为BD上任意一点),得到△ABE和△ADE纸片;
第二步:如图②,将△ABE纸片平移至△DCF处,将△ADE纸片平移至△BCG处;
第三步:如图③,将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ与DC重合,△PQM和△DCF在DC同侧),将△BCG纸片翻转过来使其背面朝上置于△PRN处,(边PR与BC重合,△PRN和△BCG在BC同侧).
则由纸片拼成的五边形PMQRN中,对角线MN长度的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,直线
 与
与 轴分别交于点
轴分别交于点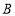 、点
、点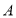 ,直线
,直线 交
交 于点
于点 ,
, 是直线
是直线 上一动点,且在点
上一动点,且在点 的上方,设点
的上方,设点 .
. 
(1)当四边形
 的面积为38时,求点
的面积为38时,求点 的坐标,此时在
的坐标,此时在 轴上有一点
轴上有一点 ,在
,在 轴上找一点
轴上找一点 ,使得
,使得 最大,求出
最大,求出 的最大值以及此时点
的最大值以及此时点 坐标;
坐标;(2)在第(1)问条件下,直线
 左右平移,平移的距离为
左右平移,平移的距离为 . 平移后直线上点
. 平移后直线上点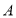 ,点
,点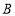 的对应点分别为点
的对应点分别为点 、点
、点 ,当
,当 为等腰三角形时,直接写出
为等腰三角形时,直接写出 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】探索规律,观察下面算式,解答问题.
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52;
…
(1)请猜想:1+3+5+7+9+…+19=________;
(2)请猜想:1+3+5+7+9+…+(2n-1)=________;
(3)试计算:101+103+…+197+199.
-
科目: 来源: 题型:
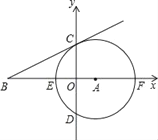
查看答案和解析>>【题目】在直角坐标系中,⊙A的半径为4,圆心A的坐标为(2,0),与x轴交于E、F两点,与y轴交于C、D两点,过点C作⊙A的切线BC,交x轴于B.
(1)求直线CB的解析式;
(2)若抛物线y=ax2+bx+c的顶点在直线BC上,与x轴交的点恰为⊙A与x轴的交点,求该抛物线的解析式;
(3)试判断C是否在抛物线上?
相关试题

