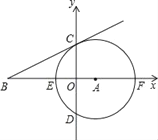
【题目】在直角坐标系中,⊙A的半径为4,圆心A的坐标为(2,0),与x轴交于E、F两点,与y轴交于C、D两点,过点C作⊙A的切线BC,交x轴于B.
(1)求直线CB的解析式;
(2)若抛物线y=ax2+bx+c的顶点在直线BC上,与x轴交的点恰为⊙A与x轴的交点,求该抛物线的解析式;
(3)试判断C是否在抛物线上?
参考答案:
【答案】(1)y=![]() x+2
x+2![]() ;
;
(2)y=﹣![]() x2+
x2+![]() x+2
x+2![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:(1)连接AC,根据圆的半径求出AC,根据点A的坐标求出OA,然后利用勾股定理列式求出OC,从而得到点C的坐标,再求出![]() 然后根据直角三角形两锐角互余求出
然后根据直角三角形两锐角互余求出![]() 再根据30°角所对的直角边等于斜边的一半求出AB的长度,然后求出OB,从而得到点B的坐标,设直线BC的解析式为
再根据30°角所对的直角边等于斜边的一半求出AB的长度,然后求出OB,从而得到点B的坐标,设直线BC的解析式为![]() 然后利用待定系数法求函数解析式解答即可;
然后利用待定系数法求函数解析式解答即可;
(2)根据圆的性质求出点![]() 然后设交点式抛物线解析式为
然后设交点式抛物线解析式为![]() 再根据抛物线的对称性确定顶点的横坐标为2,利用顶点在直线BC上求出纵坐标,然后利用待定系数法求二次函数解析式解答;
再根据抛物线的对称性确定顶点的横坐标为2,利用顶点在直线BC上求出纵坐标,然后利用待定系数法求二次函数解析式解答;
(3)把点C坐标代入抛物线解析式验证即可.
试题解析:(1)如图,连接AC,
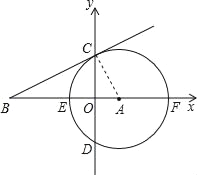
∵⊙A的半径为4,圆心A的坐标为(2,0),
∴AC=4,OA=2,
在Rt△ACO中, ![]()
∴点C的坐标为![]()
∵![]()
∴![]()
∴![]()
∴AB=2AC=2×4=8,
∴OB=ABOA=82=6,
∴点B的坐标为(6,0),
设直线BC的解析式为![]()
则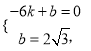
解得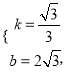
所以,直线BC的解析式为![]()
(2)∵⊙A的半径为4,圆心A的坐标为(2,0),
∴点E(2,0)、F(6,0),
∵抛物线经过点E.F,
∴顶点的横坐标为2,
∵顶点在直线BC上,
∴顶点纵坐标为![]()
∴顶点坐标为![]()
设抛物线解析式为y=a(x+2)(x6),
∴![]()
解得![]()
∴![]()
即![]()
(3)当x=0时, ![]()
所以,点![]() 在抛物线上.
在抛物线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上的点A,B,C,D,E表示连续的五个整数,对应的数分别为a,b,c,d,e.
(1)若a=-3,则e = ;
(2)若a+e=0,则代数式b+c+d= ;
(3)若d是最大的负整数,求代数式
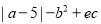 的值(写出求解过程).
的值(写出求解过程).(4)若e=4,F也为数轴上一点,且BE=2FE,则F表示的数为 ;
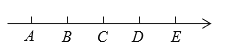
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,直线
 与
与 轴分别交于点
轴分别交于点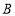 、点
、点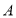 ,直线
,直线 交
交 于点
于点 ,
, 是直线
是直线 上一动点,且在点
上一动点,且在点 的上方,设点
的上方,设点 .
. 
(1)当四边形
 的面积为38时,求点
的面积为38时,求点 的坐标,此时在
的坐标,此时在 轴上有一点
轴上有一点 ,在
,在 轴上找一点
轴上找一点 ,使得
,使得 最大,求出
最大,求出 的最大值以及此时点
的最大值以及此时点 坐标;
坐标;(2)在第(1)问条件下,直线
 左右平移,平移的距离为
左右平移,平移的距离为 . 平移后直线上点
. 平移后直线上点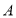 ,点
,点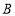 的对应点分别为点
的对应点分别为点 、点
、点 ,当
,当 为等腰三角形时,直接写出
为等腰三角形时,直接写出 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】探索规律,观察下面算式,解答问题.
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52;
…
(1)请猜想:1+3+5+7+9+…+19=________;
(2)请猜想:1+3+5+7+9+…+(2n-1)=________;
(3)试计算:101+103+…+197+199.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿AE折叠,点D的对应点落在BC上点F处,过点F作FG∥CD,连接EF,DG,下列结论中正确的有( )
①∠ADG=∠AFG;②四边形DEFG是菱形;③DG2=
 AEEG;④若AB=4,AD=5,则CE=1.
AEEG;④若AB=4,AD=5,则CE=1.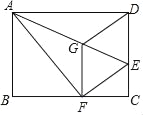
A. ①②③④ B. ①②③ C. ①③④ D. ①②
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据爱因斯坦的相对论可知,任何物体的运动速度不能超过光速(3×105km/s),因为一个物体达到光速需要无穷多的能量,并且时光会倒流,这在现实中是不可能的.但我们可让一个虚拟物超光速运动,例如:直线l,m表示两条木棒相交成的锐角的度数为10°,它们分别以与自身垂直的方向向两侧平移时,它们的交点A也随着移动(如图箭头所示),如果两条直线的移动速度都是光速的0.2倍,则交点A的移动速度是光速的_____倍.(结果保留两个有效数字).
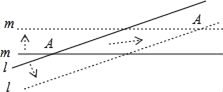
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为测量学校旗杆AB的高度,小明从旗杆正前方3米处的点C出发,沿坡度为i=1:
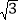 的斜坡CD前进2
的斜坡CD前进2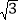 米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.(1)求点D的铅垂高度(结果保留根号);
(2)求旗杆AB的高度(精确到0.1).
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
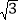 ≈1.73.)
≈1.73.)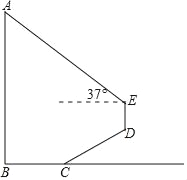
相关试题

