【题目】探索规律,观察下面算式,解答问题.
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52;
…
(1)请猜想:1+3+5+7+9+…+19=________;
(2)请猜想:1+3+5+7+9+…+(2n-1)=________;
(3)试计算:101+103+…+197+199.
参考答案:
【答案】(1)102 ;(2)n2 ;(3)7500.
【解析】
(1)观察不难发现,从1开始的连续奇数的和等于首尾两个奇数的和的一半的平方,根据此规律进行计算即可得解;
(2)观察不难发现,从1开始的连续奇数的和等于首尾两个奇数的和的一半的平方,根据此规律进行计算即可得解;
(3)用从1开始到199的和减去从1开始到99的和,然后利用前面结论进行计算即可得解.
(1)1+3+5+7+9+…+19
=![]()
=100;
(2)1+3+5+7+9+…+(2n-1)
=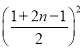
=n2;
(3)101+103+…+197+199
=(1+3+…+197+199)-(1+3+…+97+99)
=![]() -
-![]()
=1002-502
=7500.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,面积为28的平行四边形纸片ABCD中,AB=7,∠BAD=45°,按下列步骤进行裁剪和拼图.

第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△ABD和△BCD纸片,再将△ABD纸片沿AE剪开(E为BD上任意一点),得到△ABE和△ADE纸片;
第二步:如图②,将△ABE纸片平移至△DCF处,将△ADE纸片平移至△BCG处;
第三步:如图③,将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ与DC重合,△PQM和△DCF在DC同侧),将△BCG纸片翻转过来使其背面朝上置于△PRN处,(边PR与BC重合,△PRN和△BCG在BC同侧).
则由纸片拼成的五边形PMQRN中,对角线MN长度的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上的点A,B,C,D,E表示连续的五个整数,对应的数分别为a,b,c,d,e.
(1)若a=-3,则e = ;
(2)若a+e=0,则代数式b+c+d= ;
(3)若d是最大的负整数,求代数式
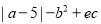 的值(写出求解过程).
的值(写出求解过程).(4)若e=4,F也为数轴上一点,且BE=2FE,则F表示的数为 ;
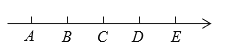
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,直线
 与
与 轴分别交于点
轴分别交于点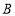 、点
、点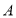 ,直线
,直线 交
交 于点
于点 ,
, 是直线
是直线 上一动点,且在点
上一动点,且在点 的上方,设点
的上方,设点 .
. 
(1)当四边形
 的面积为38时,求点
的面积为38时,求点 的坐标,此时在
的坐标,此时在 轴上有一点
轴上有一点 ,在
,在 轴上找一点
轴上找一点 ,使得
,使得 最大,求出
最大,求出 的最大值以及此时点
的最大值以及此时点 坐标;
坐标;(2)在第(1)问条件下,直线
 左右平移,平移的距离为
左右平移,平移的距离为 . 平移后直线上点
. 平移后直线上点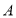 ,点
,点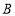 的对应点分别为点
的对应点分别为点 、点
、点 ,当
,当 为等腰三角形时,直接写出
为等腰三角形时,直接写出 的值.
的值. -
科目: 来源: 题型:
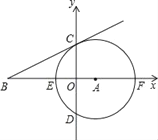
查看答案和解析>>【题目】在直角坐标系中,⊙A的半径为4,圆心A的坐标为(2,0),与x轴交于E、F两点,与y轴交于C、D两点,过点C作⊙A的切线BC,交x轴于B.
(1)求直线CB的解析式;
(2)若抛物线y=ax2+bx+c的顶点在直线BC上,与x轴交的点恰为⊙A与x轴的交点,求该抛物线的解析式;
(3)试判断C是否在抛物线上?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿AE折叠,点D的对应点落在BC上点F处,过点F作FG∥CD,连接EF,DG,下列结论中正确的有( )
①∠ADG=∠AFG;②四边形DEFG是菱形;③DG2=
 AEEG;④若AB=4,AD=5,则CE=1.
AEEG;④若AB=4,AD=5,则CE=1.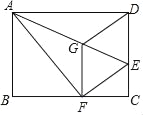
A. ①②③④ B. ①②③ C. ①③④ D. ①②
-
科目: 来源: 题型:
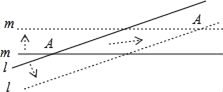
查看答案和解析>>【题目】根据爱因斯坦的相对论可知,任何物体的运动速度不能超过光速(3×105km/s),因为一个物体达到光速需要无穷多的能量,并且时光会倒流,这在现实中是不可能的.但我们可让一个虚拟物超光速运动,例如:直线l,m表示两条木棒相交成的锐角的度数为10°,它们分别以与自身垂直的方向向两侧平移时,它们的交点A也随着移动(如图箭头所示),如果两条直线的移动速度都是光速的0.2倍,则交点A的移动速度是光速的_____倍.(结果保留两个有效数字).
相关试题

