【题目】在平面直角坐标系中,O为坐标原点,点A的坐标为(a,a),点B的坐标(b,c),且a、b、c满足![]() .
.
(1)若a没有平方根,判断点A在第几象限并说明理由.
(2)连AB、OA、OB,若△OAB的面积大于5而小于8,求a的取值范围;
(3)若两个动点M(2m,3m-5),N(n-1,-2n-3),请你探索是否存在以两个动点M、N为端点的线段MN∥AB,且MN=AB.若存在,求出M、N两点的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)第三象限;(2)见解析;(3)见解析
【解析】
(1)根据平方根的意义得到a<0,然后根据各象限点的坐标点的特征可判断点A在第三象限;(2)先利用方程组![]() ,用a表示b、c,得b=2+a.c=a, 则B点的坐标为(2+a,a),故AB//x轴,AB=|2+a-a|=2,故
,用a表示b、c,得b=2+a.c=a, 则B点的坐标为(2+a,a),故AB//x轴,AB=|2+a-a|=2,故![]() 由若△OAB的面积大于5而小于8,可得
由若△OAB的面积大于5而小于8,可得![]() 计算即可得a的取值范围;
计算即可得a的取值范围;
(3)由AB//x轴即MN∥AB可得MN∥x轴,则M、N的y坐标,以及MN=AB=2,可得方程组解得m、n的值,即可得出结论;
(1)∵a没有平方根,
∴a<0,
∴点A在第三象限;
(2)解方程组![]()
用a表示b、c,得![]()
∵点B坐标为(b,c)
∴点B坐标为(2+a,a)
∵点A的坐标为(a,a)
∴AB=|2+a-a|=2,AB与x轴平行
∴![]()
∵△OAB的面积大于5而小于8,
∴![]()
解得:![]() 或
或![]()
(3) ∵AB∥x轴
又∵MN∥AB
∴MN∥x轴
∵M(2m, 3m-5) N(n-1, -2n-3), MN=AB=2
∴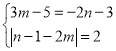
∴![]()
![]()
∴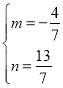 或
或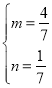
∴![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 在平面直角坐标系xOy中,三角形ABC三个顶点的坐标分别为(-2,-2),(3,1),(0,2),若把三角形ABC向上平移 3 个单位长度,再向左平移
 个单位长度得到三角形
个单位长度得到三角形  ,点A,B,C的对应点分别为
,点A,B,C的对应点分别为  ,
, ,
, .
.(1)写出点
 ,
, ,
, 的坐标;
的坐标;(2)在图中画出平移后的三角形
 ;
;(3)三角形
 的面积为__________.
的面积为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对非负实数x“四含五入”到个位的值记为
 ,即当n为非负整数时,若n-
,即当n为非负整数时,若n-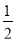 ≤x<n+
≤x<n+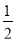 ,则
,则 =n.如:
=n.如: ,
, ,……根据以上材料,解决下列问题:
,……根据以上材料,解决下列问题:(1)填空
 = ,
= , = ;
= ;(2)若
 ,则x的取值范围是 ;
,则x的取值范围是 ;(3)求满足
 的所有实数x的值.
的所有实数x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(14分)如图,已知抛物线
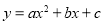 (
( )与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
(1)求此抛物线的解析式;
(2)若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求出此时点E的坐标;
(3)点P在抛物线的对称轴上,若线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在正方形
 外取一点
外取一点 ,连接
,连接 、
、 、
、 .过点
.过点 作
作 的垂线交
的垂线交 于点
于点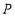 .若
.若 ,
, .下列结论:①
.下列结论:① ;②点
;②点 到直线
到直线 的距离为
的距离为 ;③
;③ ;④
;④ ;⑤
;⑤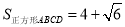 ;其中正确结论的序号是( )
;其中正确结论的序号是( )
A.①③④B.①②⑤C.③④⑤D.①③⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点C的对应点C′.(利用网格点和三角板画图)
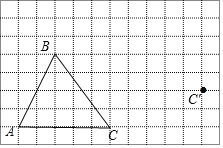
(1)画出平移后的△A′B′C′.
(2)画出AB边上的中线线CD;
(3)在整个平移过程中,线段BC扫过的面积是___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次数学兴趣小组活动中,同学们做了一个找朋友的游戏:有六个同学A、B、C、D、E、F分别藏在六张大纸牌的后面,如图,A、B、C、D、E、F所持的纸牌的前面分别写有六个算式:66;63+63;(63)3;(2×62)×(3×63);(22×32)3;(64)3÷62.游戏规定:所持算式的值相等的两个人是朋友.如果现在由同学A来找他的朋友,他可以找谁呢?说说你的看法.
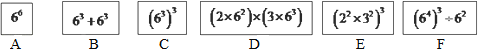
相关试题

